세마포어
다양한 범주의 병행성 문제 해결을 위해서는 락과 조건 변수가 모두 필요하다. 정확한 역사를 파악하기는 어렵지만, 이 사실을 최초로 인지한 사람 중에 Edsger Dijkstra(우리말로 "다이직스트라"라고 발음하면 대략 비슷하다)가 있다 [GR92]. 그는 "최단 경로" 알고리즘이라고 하는 그래프 이론으로 유명할 뿐만 아니라 [Dij59] "Goto 문의 유해성 (Goto Statements Considered Harmful)"(제목이 정말 멋있다!) 이라는 구조화 프로그래밍에 관한 격렬한 논쟁을 이끌어낸 것으로도 유명하다 [Dij68a]. 이번 장에서 다루게 될 세마포어(semaphore)라는 동기화 기법도 그가 개발한 것이다 [Dij68b]; [Dij72]. Dijkstra와 그의 동료들은 모든 다양한 동기화 관련 문제를 한 번에 해결할 수 있는 그런 기법을 개발하고자 했다. 그리고 세마포어가 탄생했다. 실로 엄청난 사건이 아니라 할 수 없다. 이제 보게 되겠지만, 세마포어는 락과 컨디션 변수로 모두 사용할 수 있다.
핵심 질문 : 세마포어를 어떻게 사용하는가 락과 컨디션 변수 대신에 세마포어를 사용하는 방법은 무엇인가? 세마포어의 정의는 무엇인가? 이진 세마포어는 무엇인가? 락과 컨디션 변수를 사용하여 세마포어를 만드는 것이 가능한가? 그 반대로 세마포어를 사용하여 락과 조건 변수를 만드는 것이 가능한가?
31.1 세마포어 : 정의
세마포어는 정수 값을 갖는 객체로서 두 개의 루틴으로 조작할 수 있다. POSIX 표준에서 이 두 개의 루틴은 sem_wait()와 sem_post()1이다. 세마포어는 초기값에 의해 동작이 결정되기 때문에, 사용하기 전 "가장 먼저" 값을 초기화를 해야 한다. 그림 31.1에서 그 코드를 나타낸다.
#include <semaphore.h>
sem_t s;
sem_init(&s, 0, 1);
그림 31.1 세마포어 초기화
이 그림에서는 세마포어 s을 선언 후, 3번째 인자로 1을 전달하여 세마포어의 값을 1로 초기화한다. sem_init()의 두 번째 인자는 모든 예제에서 0 이다. 이 값은 같은 프로세스 내의 쓰레드 간에 세마포어를 공유한다는 것을 의미한다. 두 번째 인자에 다른 값을 사용하는 예(다른 프로세스 간에 동기화를 제공하는 방법과 같은)는 세마포어의 용법에 대한 매뉴얼을 읽어보기를 바란다.
초기화된 후에는 sem_wait(), 또는 sem_post()라는 함수를 호출하여 세마포어를 다룰 수 있다. 이 두 함수의 동작은 그림 31.2에 나타내었다.
int sem_wait(sem_t *s) {
decrement the value of semaphore s by one;
wait if value of semaphore s is negative;
}
int sem_post(sem_t *s) {
increment the value of semaphore s by one;
if there are one or more threads waiting, wake one;
}
그림 31.2 세마포어: sem_wait()과 sem_post()의 정의
이 루틴들은 다수 쓰레드들에 의해 동시에 호출되는 것을 가정한다. 임계 영역은 적절히 보호되어야 한다. 뒷골이 살짝 땡기기 시작한다. 임계 영역 보호에 대한 고민은 잠시 후로 미루자. 휴우, 살았다. 그치? 지금은 이 두 함수의 사용 방법에 집중하자. 이 두 함수를 어떻게 만들어야 하는지에 대한 고민은 추후에 하자.
우선 몇 가지 핵심적인 성질을 논의해 보자. 첫 번째로, sem_wait() 함수는 즉시 리턴하거나 (세마포어의 값이 1이상이면), 아니면 해당 세마포어 값이 1이상이 될 때까지 호출자를 대기시킨다. 다수의 쓰레드들이 sem_wait()를 호출할 수 있기 때문에, 대기큐에는 다수의 쓰레드가 존재할 수 있다. 대기하는 법에는 회전(spin)과 재우기(sleep)의 두 가지가 있다는 것을 상기하자.
두 번째, sem_wait() 함수와 달리 sem_post() 함수는 대기하지 않는다. 세마포어 값을 증가시키고 대기 중인 쓰레드 중 하나를 깨운다.
세 번째로, 세마포어가 음수라면 그 값은 현재 대기 중인 쓰레드의 개수와 같다 [Dij68b]. 일반적으로 세마포어 사용자는 이 값을 알 수 없다. 하지만, 이러한 성질을 알고 있는 것이 세마포어 작동을 이해하는 데 도움이 된다.
이 두 개의 함수는 원자적으로 실행된다고 가정한다. 세마포어 루틴 내에서 레이스 컨디션이 발생할 수 있다는 사실은 (아직은) 걱정하지 말자. 그것을 해결하기 위해 곧 락과 컨디션 변수를 사용하게 될 것이다.
31.2 이진 세마포어(락)
이제 세마포어를 사용할 준비가 되었다. 우리가 처음으로 세마포어를 적용할 곳은 이미 친숙한 "락"이다. 그림 31.3에 코드가 있다. sem_wait()/sem_post() 쌍으로 임계 영역 부분을 둘러싼 것을 볼 수 있다. 이것이 동작하기 위한 핵심은 세마포어 m의 초기값이다 (그림에서는 X로 초기화가 되었다). 이 X의 값이 무엇이 되어야 하겠는가?
sem_t m;
sem_init(&m, 0, X); // X로 세마포어를 초기화하기. 이때 X가 가져야 할 값은?
sem_wait(&m);
// 임계 영역 부분은 여기에 배치
sem_post(&m);
그림 31.3 이진 세마포어(또는, 락)
... (계속 진행하기에 앞서 좀 더 생각해 보자) ...
sem_wait()와 sem_post()의 정의를 되새겨보면 초기값은 1이 되어야 한다는 것을 알 수 있다.
이 부분을 분명하게 하기 위해 쓰레드가 두 개인 경우를 생각해 보자. 첫 쓰레드 (쓰레드 0)가 sem_wait()를 호출한다. 먼저 세마포어 값을 1 감소시켜 0으로 만든다. 쓰레드는 세마포어 값이 음수인 경우에만 대기한다. 세마포어의 값이 0이므로 리턴하고 진행할 수 있다. 쓰레드 0은 이제 임계 영역에 진입할 수 있다. 쓰레드 0이 임계 영역내에 있을 때 다른 쓰레드가 락을 획득하려고 하지 않는다면, 이 쓰레드가 sem_post()를 불렀을 때 세마포어 값이 다시 1로 설정된다(대기 중인 쓰레드가 없기 때문에, 아무도 깨우지 않는다). 그림 31.4에 이 시나리오의 흐름이 나타나 있다.
| 세마포어의 값 | 쓰레드 0(T0) | 쓰레드 1(T1) |
|---|---|---|
| 1 | ||
| 1 | sem_wait()를 호출 | |
| 0 | sem_wait() 리턴 | |
| 0 | (임계 영역) | |
| 0 | sem_post()를 호출 | |
| 1 | sem_post 리턴 |
그림 31.4 쓰레드의 흐름: 세마포어를 사용하는 하나의 쓰레드
좀 더 흥미로운 상황은 쓰레드 0이 "락을 보유하고"있을 때 (sem_wait()를 호출하여 임계 영역에 진입했지만 아직 sem_post()를 호출하지 않은 경우) 다른 쓰레드(쓰레드 1)가 sem_wait()를 호출하여 임계 영역 진입을 시도하는 경우이다. 이 경우 쓰레드 1이 세마포어 값을 -1로 감소시키고 대기에 들어간다(프로세서를 내어주고 스스로 잠자기에 들어간다). 쓰레드 0이 다시 실행되면 sem_post()를 호출하고, 세마포어 값을 0으로 증가시키고, 잠자던 쓰레드 (쓰레드 1)를 깨운다. 그러면 쓰레드 1이 락을 획득할 수 있게 된다. 쓰레드 1의 작업이 끝나면, 세마포어의 값을 다시 증가시켜 1이 되도록 한다.
그림 31.5는 이 예제의 흐름을 나타낸다. 쓰레드들의 동작 외에도 각 쓰레드의 상태도 같이 나타낸다. 상태는 실행, 준비 (실행할 수 있지만 아직은 실행되지 않은 상태), 그리고 대기로 표현되었다. 누군가가 보유하고 있는 락을 획득하려고 할 때 쓰레드 1이 대기 상태에 들어가는 것에 유의한다. 쓰레드 0이 다시 실행이 될 때에만 쓰레드 1이 깨어나서 실행 가능한 상태가 된다.
혼자 좀 더 공부하고자 한다면, 하나의 락을 여러 개의 쓰레드가 기다리는 경우를 생각해 보라. 그 상황에서는 세마포어의 값이 어떻게 변화할까?
세마포어를 락으로 쓸 수 있다는 것을 알았다. 락은 두 개의 상태 (사용 가능, 사용 중) 만 존재하므로 이진 세마포어 (binary semaphore)라고도 불린다. 만약 세마포어를 이진 세마포어로만 사용할 목적이라면, 현재 우리가 설명하는 범용 세마포어2보다 더 쉽게 구현할 수 있다.
| 세마포어의 값 | 쓰레드 0(T0) | 상태 | 쓰레드 1(T1) | 상태 |
|---|---|---|---|---|
| 1 | 실행 | 준비 | ||
| 1 | sem_wait()를 호출 | 실행 | 준비 | |
| 0 | sem_wait() 리턴 | 실행 | 준비 | |
| 0 | (임계 영역 : 시작) | 실행 | 준비 | |
| 0 | 인터럽트 ; T1으로 변경 | 준비 | 실행 | |
| 0 | 준비 | sem_wait()를 호출 | 실행 | |
| -1 | 준비 | sem 감소 | 실행 | |
| -1 | 준비 | (sem < 0)이기 때문에 대기 | 대기 | |
| -1 | 실행 | T0으로 변경 | 대기 | |
| -1 | (임계 영역 : 끝) | 실행 | 대기 | |
| -1 | sem_post() 호출 | 실행 | 대기 | |
| 0 | sem 증가 | 실행 | 대기 | |
| 0 | wake(T1) | 실행 | 준비 | |
| 0 | sem_post() 리턴 | 실행 | 준비 | |
| 0 | 인터럽트 ; T1으로 변경 | 준비 | 실행 | |
| 0 | 준비 | sem_wait() 리턴 | 실행 | |
| 0 | 준비 | (임계 영역 : 시작) | 실행 |
그림 31.5 쓰레드의 흐름 : 세마포어를 사용하는 두 개의 쓰레드
31.3 컨디션 변수로서의 세마포어
어떤 조건이 참이 되기를 기다리기 위해 현재 쓰레드를 멈출 때에도 세마포어는 유용하게 사용될 수 있다. 예를 들어, 리스트에서 객체를 삭제하기 위해 리스트에 객체가 추가되기를 대기하는 쓰레드가 있을 수 있다. 이런 종류의 전형적인 패턴이 하나의 쓰레드가 어떤 사건의 발생을 기다리고, 또 다른 쓰레드는 해당 사건을 발생시킨 후, 시그널을 보내어 기다리는 쓰레드를 깨우는 것이다. 대기 중인 쓰레드(또는 쓰레드들)가 프로그램에서의 어떤 조건(condition)이 만족되기를 대기하기 때문에, 세마포어를 컨디션 변수처럼 사용할 수 있다.
다음과 같은 간단한 예제를 보자. 그림 31.6과 같이 부모 쓰레드가 자식 쓰레드를 생성한 후, 자식 쓰레드의 종료를 대기하고자 한다. 이 프로그램이 실행하여 다음과 같은 결과를 얻고자 한다.
parent: begin
child
parent: end
sem_t s;
void *child(void *arg) {
printf("child\n");
sem_post(&s); // 시그널 전달: 자식의 동작이 끝남
return NULL;
}
int main(int argc, char *argv[]) {
sem_init(&s, 0, X); // X의 값은 무엇이 되어야 할까?
printf("parent: begin\n");
pthread_t c;
pthread_create(&c, NULL, child, NULL);
sem_wait(&s); // 자식을 여기서 대기
printf("parent: end\n");
return 0;
}
그림 31.6 자식을 대기 중인 부모
세마포어를 이용하여 어떻게 이 효과를 만들 수 있을까? 답은 의외로 간단하다. 코드에서 볼 수 있듯이, 부모 프로세스는 자식 프로세스 생성 후 sem_wait()를 호출하여 자식의 종료를 대기한다. 자식은 sem_post()를 호출하여 종료되었음을 알린다. 중요한 질문이 있다. 세마포어 값을 무엇으로 초기화할까?
(잠깐! 생각을 충분히 하고 계속 읽자.)
정답 : 세마포어의 초기값은 0이다. 두 가지 상황이 발생할 수 있다. 첫 번째, 자식 프로세스 생성 후, 아직 자식 프로세스가 실행을 시작하지 않은 경우다 (준비 큐에만 들어 있고 실행 중이 아니다). 이 경우 (그림 31.7), 자식이 sem_post()를 호출하기 전에 부모가 sem_wait()를 호출할 것이다. 부모 프로세스는 자식이 실행될 때까지 대기해야 한다. 이를 위해서는 wait() 호출 전에 세마포어 값이 0보다 같거나 작아야 한다. 때문에 0이 초기값이 되어야 한다. 부모가 실행되면 세마포어 값을 감소시키고 (-1로) 대기한다. 자식이 실행되었을 때 sem_post()를 호출하여 세마포어의 값을 0으로 증가시킨 후 부모를 깨운다. 그러면 부모는 sem_wait()에서 리턴을 하여 프로그램을 종료시킨다.
| 값 | 부모(Parent) | 상태 | 자식(Child) | 상태 |
|---|---|---|---|---|
| 0 | create(Child) | 실행 | (Child 존재 ; 실행 가능함) | 준비 |
| 0 | sem_wait() 호출 | 실행 | 준비 | |
| -1 | sem 감소 | 실행 | 준비 | |
| -1 | (sem < 0)이기 때문에 대기 | 대기 | 준비 | |
| -1 | Child로 변경 | 대기 | Child 실행 | 실행 |
| -1 | 대기 | sem_post() 호출 | 실행 | |
| 0 | 대기 | sem 증가 | 실행 | |
| 0 | 준비 | wake(Parent) | 실행 | |
| 0 | 준비 | sem_post() 리턴 | 실행 | |
| 0 | 인터럽트 ; parent로 변경 | 실행 | 준비 | |
| 0 | sem_wait() 리턴 | 실행 | 준비 |
그림 31.7 자식을 기다리는 부모 (사례 1)
두 번째 경우는 (그림 31.8) 부모 프로세스가 sem_wait()를 호출하기 전에 자식 프로세스의 실행이 종료된 경우이다. 이 경우, 자식이 먼저 sem_post()를 호출하여 세마포어의 값을 0에서 1로 증가시킨다. 부모가 실행할 수 있는 상황이 되면 sem_wait()를 호출한다. 세마포어 값이 1인 것을 발견할 것이다. 부모는 세마포어 값을 0으로 감소시키고 sem_wait()에서 대기 없이 리턴한다. 이 방법 역시 의도한 결과를 만들어 낸다.
| 값 | 부모(Parent) | 상태 | 자식(Child) | 상태 |
|---|---|---|---|---|
| 0 | create(Child) | 실행 | (Child 존재 ; 실행 가능함) | 준비 |
| 0 | 인터럽트; Child로 변경 | 준비 | Child 실행 | 실행 |
| 0 | 준비 | sem_post() 호출 | 실행 | |
| 1 | 준비 | sem 증가 | 실행 | |
| 1 | 준비 | wake(nobody) | 실행 | |
| 1 | 준비 | sem_post() 리턴 | 실행 | |
| 1 | parent 실행 | 실행 | 인터럽트; parent로 변경 | 준비 |
| 1 | sem_wait() 호출 | 실행 | 준비 | |
| 0 | sem 감소 | 실행 | 준비 | |
| 0 | (sem < 0)이기 때문에 대기 | 실행 | 준비 | |
| 0 | sem_wait() 리턴 | 실행 | 준비 |
그림 31.8 자식을 기다리는 부모(사례 2)
31.4 생산자/소비자 (유한 버퍼) 문제
다음 문제는 생산자/소비자 문제 또는 유한 버퍼라고 불리는 문제이다 [Dij72]. 이 문제는 이전 장에서 상세히 설명하였으므로 구체적인 내용은 이전 장을 참고하기 바란다.
첫 번째 시도
이 문제를 해결하는 첫 번째 시도에서는 empty와 full이라는 두 개의 세마포어를 사용한다. 쓰레드는 empty와 full을 사용하여 버퍼 공간이 비었는지 채워졌는지를 표시한다. put()과 get() 코드는 그림 31.9에 나타내었고 생산자와 소비자 문제를 해결하기 위해 시도한 해법은 그림 31.10에 나타내었다.
int buffer[MAX];
int fill = 0;
int use = 0;
void put(int value) {
buffer[fill] = value; // f1 라인
fill = (fill + 1) % MAX; // f2 라인
}
int get() {
int tmp = buffer[use]; // g1 라인
use = (use + 1) % MAX; // g2 라인
return tmp;
}
그림 31.9 put()과 get() 루틴
이 예제에서 생산자는 버퍼가 비워져서 데이터를 넣을 수 있기를 기다리고, 마찬가지로 소비자는 데이터를 꺼내기 위해 버퍼가 채워지기를 기다린다. MAX=1인 상황(버퍼의 크기가 1인 경우)이 어떻게 동작할지 생각해 보자.
생산자와 소비자 쓰레드가 각 하나씩 있고 CPU도 하나인 상황에 대해 살펴보자. 소비자가 먼저 실행했다고 가정하면 소비자 쓰레드가 그림에서 C1 라인에 먼저 도달하여 sem_wait(&full)을 호출한다. 변수 full의 값은 0으로 초기화되었기 때문에 해당 명령으로 인해 full의 값은 -1로 감소되고, 소비자는 대기한다. 다른 쓰레드가 sem_post()를 호출해서 full 변수가 증가하기를 기다려야 한다.
sem_t empty;
sem_t full;
void *producer(void *arg) {
int i;
for (i = 0; i < loops; i++) {
sem_wait(&empty); // P1 라인
put(i); // P2 라인
sem_post(&full); // P3 라인
}
}
void *consumer(void *arg) {
int i, tmp = 0;
while (tmp != -1) {
sem_wait(&full); // C1 라인
tmp = get(); // C2 라인
sem_post(&empty); // C3 라인
printf("%d\n", tmp);
}
}
int main(int argc, char *argv[]) {
// ...
sem_init(&empty, 0, MAX); // MAX 버퍼는 비어 있는 상태로 시작...
sem_init(&full, 0, 0); // ... 그리고 0이 가득 참
// ...
}
그림 31.10 full과 empty 조건 추가하기
그런 이후에 생산자 쓰레드가 실행하여 P1 라인에서 sem_wait(&empty) 루틴을 호출한다. empty 변수가 MAX (이 경우에는 1)로 설정되었기 때문에 소비자와 다르게 생산자는 다음 문장을 계속 실행한다. empty 변수는 감소하여 0이 되고 생산자가 데이터 값을 버퍼의 첫 번째 공간에 넣는다(P2 라인). 그런 후에 생산자는 P3 라인의 sem_post(&full)를 호출하여 세마포어의 full의 세마포어의 값을 -1에서 0으로 변경하고 소비자 쓰레드를 깨운다(대기 상태에서 준비 상태로 바뀐다).
위의 알고리즘에서 둘 중 하나의 상황이 발생할 수 있다. 생산자가 계속 실행한다면 반복문을 돌아 P1 라인을 다시 실행하게 된다. empty 세마포어의 값이 0이므로 대기상태로 들어간다. 생산자 프로세스가 인터럽트에 걸리고 소비자 쓰레드가 실행된다면 sem_wait(&full) 문(C1 라인)을 호출하면서 버퍼가 찼다는 것을 발견하고 데이터를 소비한다. 어느 경우이든 원하는 결과를 얻을 수 있다. 이 경우를 다수의 쓰레드(다수의 생산자와 소비자의 경우)로 확장하여 검증해 볼 수 있다. 그래도 여전히 제대로 동작할 것이다.
이번에는 MAX 값이 1보다 크고(MAX=10), 또한 생산자와 소비자 쓰레드들이 여러 개 있다고 하자. 경쟁 조건이 발생한다. 어디에서 경쟁이 발생하는지 찾을 수 있겠는가? 시간을 들여 찾아보자. 만약 못 찾겠다면, 힌트는 put()과 get() 코드를 유심히 살펴봐야 한다.
오케이, 문제를 들여다보자. 두 개의 생산자 Pa와 Pb가 있는데, 두 쓰레드가 put()을 거의 동시에 호출하였다고 해 보자. Pa가 먼저 실행되어서 버퍼에 첫 공간에 값을 넣기 시작한다(f1 라인에서 fill=0이다). Pa 쓰레드가 fill 카운터 변수가 1로 변경하기 전에 인터럽트가 걸렸다. 생산자 Pb가 실행되고 f1 라인에서 마찬가지로 버퍼의 첫 번째 공간에 데이터를 삽입한다. Pa가 기록한 이전의 값은 새로운 값으로 대체된다! 이렇게 되면 절대 안 된다. 생산자의 데이터의 어느 것도 사라지면 안 된다.
해답: 상호 배제의 추가
짐작하겠지만, 위에서 상호 배제를 고려하지 않았다. 버퍼를 채우고 버퍼에 대한 인덱스를 증가하는 동작은 임계 영역이기 때문에 신중하게 처리해야 한다. 지금까지 배운 이진 세마포어와 몇 개의 락을 추가하여 해결해 보자. 그림 31.11에 그 시도가 나타나 있다.
sem_t empty;
sem_t full;
sem_t mutex;
void *producer(void *arg) {
int i;
for (i = 0; i < loops; i++) {
sem_wait(&mutex); // p0 라인(추가됨)
sem_wait(&empty); // p1 라인
put(i); // p2 라인
sem_post(&full); // p3 라인
sem_post(&mutex); // p4 라인(추가됨)
}
}
void *consumer(void *arg) {
int i;
for (i = 0; i < loops; i++) {
sem_wait(&mutex); // c0 라인(추가됨)
sem_wait(&full); // c1 라인
int tmp = get(); // c2 라인
sem_post(&empty); // c3 라인
sem_post(&mutex); // c4 라인(추가됨)
printf("%d\n", tmp);
}
}
int main(int argc, char *argv[]) {
// ...
sem_init(&empty, 0, MAX); // MAX 버퍼는 비어 있는 상태로 시작...
sem_init(&full, 0, 0); // ... 그리고 0 이 가득 참
sem_init(&mutex, 0, 1); // 락이기 때문에 mutex=1 (추가됨)
// ...
}
그림 31.11 상호 배제 추가하기 (잘못된 방법)
이제 put()/get() 코드에 락을 추가했으며 추가된 라인은 추가됨이라고 표기해놓았다. 괜찮은 발상인 것 같은데, 아직도 동작하지 않는다. 왜일까? 교착 상태이다. 교착 상태는 왜 발생할까? 잠시 생각해 보자. 교착 상태가 발생하는 경우를 찾아보자. 프로그램이 어떤 순서로 동작하면 교착 상태가 발생할까?
교착 상태의 방지
여기 정답이 있다. 생산자와 소비자 쓰레드가 각 하나씩 있다고 하자. 소비자가 먼저 실행이 되었다. mutex(c0 라인)를 획득하고 full 변수에 대하여 sem_wait() (c1 라인)를 호출한다. 아직 데이터가 없기 때문에 소비자는 대기해야 하고 CPU를 양보해야 한다. 여기서 중요한 것은 소비자가 아직도 락을 획득하고 있다는 것이다.
생산자가 실행된다. 실행이 가능하면 데이터를 생성하고 소비자 쓰레드를 깨울 것이다. 불행하게도 이 쓰레드는 먼저 mutex 세마포어에 대해서 sem_wait()를 실행한다(p0 라인). 이미 락은 소비자가 획득한 상태이기 때문에 생산자 역시 대기에 들어간다.
순환 고리가 생겼다. 소비자는 mutex를 갖고 있으면서 다른 full 시그널을 발생시키기를 대기하고 있다. full 시그널을 발생시켜야 하는 생산자는 mutex에서 대기 중이다. 생산자와 소비자가 서로를 기다린다. 전형적인 교착 상태이다.
최종, 제대로 된 해법
이 문제를 해결하기 위해서는 락의 범위(scope)를 줄여야 한다. 그림 31.12가 최종 해답이다. 보는 바와 같이, mutex를 획득하고 해제하는 코드를 임계 영역 바로 이전과 이후로 이동하였다. full이나 empty와 관련된 코드는 mutex 밖으로 배치하였다.
sem_t empty;
sem_t full;
sem_t mutex;
void *producer(void *arg) {
int i;
for (i = 0; i < loops; i++) {
sem_wait(&empty); // p1 라인
sem_wait(&mutex); // p1.5 라인(여기로 MUTEX 이동)
put(i); // p2 라인
sem_post(&mutex); // p2.5 라인(... 그리고 여기)
sem_post(&full); // p3 라인
}
}
void *consumer(void *arg) {
int i;
for (i = 0; i < loops; i++) {
sem_wait(&full); // c1 라인
sem_wait(&mutex); // c1.5 라인(여기로 MUTEX 이동)
int tmp = get(); // c2 라인
sem_post(&mutex); // c2.5 라인 (... 그리고 여기)
sem_post(&empty); // c3 라인
printf("%d\n", tmp);
}
}
int main(int argc, char *argv[]) {
// ...
sem_init(&empty, 0, MAX); // MAX 버퍼는 비어 있는 상태로 시작...
sem_init(&full, 0, 0); // ... 그리고 0이 가득참
sem_init(&mutex, 0, 1); // 락이기 때문에 mutex=1
// ...
}
그림 31.12 상호 배제 추가하기(올바른 방법)
결과 멀티 쓰레드 프로그램에서 사용 가능한 유한 버퍼를 만들었다. 지금은 이해만 하고, 나중에 활용하자. 앞으로 두고두고 고마워하게 될 것이다. 최소한, 기말 고사에 같은 질문이 나왔을 때 고마워하게 될 것이다.
31.5 Reader-Writer 락
또 하나의 고전적인 문제가 있다. 좀 더 융통성 있는 락 기법이 필요하다. 다양한 자료 구조를 접근하는 데 여러 종류의 락 기법이 필요하다. 리스트에 삽입하고 간단한 검색을 하는 것과 같은 병행연산이 여러 개 있다고 해 보자. 삽입 연산은 리스트의 상태를 변경하고(전통적인 임계 영역 보호 방식으로 해결 가능하다), 검색은 자료 구조를 단순히 읽기만 한다. 삽입 연산이 없다는 보장만 된다면 다수의 검색 작업을 동시에 수행할 수 있다. 이와 같은 경우를 위해 만들어진 락이 reader-writer 락이다 [CHP71]. 이 락에 대한 코드는 그림 31.13에 나타나 있다.
typedef struct _rwlock_t {
sem_t lock; // 이진 세마포어 (기본 락)
sem_t writelock; // 하나의 쓰기 또는 다수의 읽기 락을 위한 락
int readers; // 임계 영역 내에 읽기를 수행 중인 reader의 수
} rwlock_t;
void rwlock_init(rwlock_t *rw) {
rw->readers = 0;
sem_init(&rw->lock, 0, 1);
sem_init(&rw->writelock, 0, 1);
}
void rwlock_acquire_readlock(rwlock_t *rw) {
sem_wait(&rw->lock);
rw->readers++;
if (rw->readers == 1)
sem_wait(&rw->writelock); // 읽기용 락이 writelock을 획득
sem_post(&rw->lock);
}
void rwlock_release_readlock(rwlock_t *rw) {
sem_wait(&rw->lock);
rw->readers--;
if (rw->readers == 0)
sem_post(&rw->writelock); // 마지막으로 읽기용 락이 writelock 해제
sem_post(&rw->lock);
}
void rwlock_acquire_writelock(rwlock_t *rw) {
sem_wait(&rw->writelock);
}
void rwlock_release_writelock(rwlock_t *rw) {
sem_post(&rw->writelock);
}
그림 31.13 간단한 reader-writer 락
이 코드는 간단하다. 자료 구조를 "갱신"하려면 새로운 동기화 연산 쌍을 사용한다. 락을 획득하기 위해서는 rwlock_acquire_writelock()을 사용하고 해제하기 위해서 rwlock_release_writelock()을 사용한다. 내부적으로는 writelock 세마포어를 사용하여 하나의 쓰기 쓰레드만이 락을 획득할 수 있도록 하여, 임계 영역 진입 후에 자료 구조를 갱신한다.
팁 : 단순무식이 더 좋을 수도 있다 (Hill's Law) 단순무식한 방법이 최고가 될 수 있다는 것을 절대로 과소평가해서는 안 된다. 락에 있어서 때로는 간단한 스핀 락이 가장 잘 동작할 수도 있다. 왜냐하면 구현이 쉽고 간단하기 때문이다. 읽기-쓰기 락과 같은 것이 듣기에는 멋져 보일 수는 있지만 복잡하다. 복잡한 것들은 느리다. 그러므로 단순무식한 방법을 가장 먼저 시도해 보자. 간단한 것이 매력적이다는 개념은 여러 곳에서 발견할 수 있다. 이 개념에 대해 초기 주장으로 CPU의 캐시 설계를 주제로 한 Mark Hill의 학위 논문을 꼽을 수 있다 [Hil87]. 그는 간단한 직접 매핑된 캐시 (direct-mapped caches)가 복잡한 집합 연관 (set-associative) 설계보다 더 잘 동작하는 것을 발견하였다 (그 이유 중 하나는 간단한 설계가 캐시에서 빠른 검색을 가능하게 한다는 것이다). Hill이 자신의 논문에서 간단하게 정리한 것처럼 "크고 무식한 것이 좋다." 그래서 이와 비슷한 충고를 Hill's Law라고 부른다.
좀 더 재미있는 부분은 읽기 락 (reader lock)의 획득과 해제이다. 읽기 락을 획득시 읽기 쓰레드 (reader)가 먼저 락을 획득하고 읽기 중인 쓰레드의 수를 표현하는 reader 변수를 증가시킨다. 첫 번째 읽기 쓰레드가 읽기 락을 획득할 때 중요한 과정이 있다. 읽기 락을 획득시 writelock 세마포어에 대해 sem_wait()을 호출하여 쓰기 락을 함께 획득한다. 획득한 쓰기 락은 읽기 락을 해제할 때 sem_post()로 다시 해제한다.
이 과정을 통해서 읽기 락을 획득하고 난 후, 다른 읽기 쓰레드들이 읽기 락을 획득할 수 있도록 한다. 다만, 쓰기 락을 획득하려는 쓰기 쓰레드 (writer)들은 모든 읽기 쓰레드가 끝날 때까지 대기하여야 한다. 임계 영역을 빠져나오는 마지막 읽기 쓰레드가 writelock에 대한 sem_post()를 호출하여 대기 중인 쓰기 쓰레드가 락을 획득할 수 있도록 한다.
이 방식은 (의도한 대로) 동작하지만 몇 가지 단점이 있는데, 특히 공정성에 문제가 있다. 상대적으로 쓰기 쓰레드가 불리하다. 쓰기 쓰레드에게 기아 현상 (starvation)이 발생하기 쉽다는 문제이다. 이에 대해서는 좀 더 세련된 해법이 존재한다. 당신도 더 좋은 구현 방법을 만들 수 있다. 힌트는 쓰기 쓰레드가 대기 중일 때는 읽기 쓰레드가 락을 획득하지 못하도록 하는 것이다. 어떻게 하면 될까? 생각해 보기 바란다.
마지막으로 읽기-쓰기 락을 사용할 때는 약간의 주의가 필요하다. 기법이 정교할수록 오버헤드가 크다는 사실이다. 때문에 단순하고 빠른 락 종류를 사용하는 것보다 항상 성능이 좋은 것은 아니다 [CB08]. 어쨌거나, 이제까지 세마포어를 사용하는 방법을 배웠다.
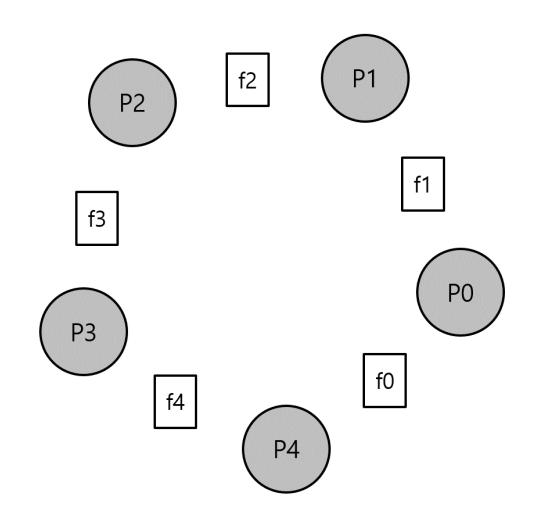
그림 31.14 식사하는 철학자
31.6 식사하는 철학자
Dijkstra가 제기한 식사하는 철학자 (Dining Philosopher) 라는 유명한 문제가 있다 [Dij71]. 이 문제가 유명한 이유는 재미있기도 하고 지적인 흥미를 유발하기 때문이다. 실제 활용도는 매우 낮다. 하지만, 너무도 유명하기 때문에 이 장에서 다루어 보고자 한다. 사실, 이 문제가 면접 질문으로 나올 수도 있다. 답변을 못해서 직장을 못 구했다면, 운영체제 교수를 원망할지 모른다. 반대로, 직장을 구했다면 운영체제 교수에게 감사의 편지나 스톡옵션 보내는 것을 망설이지 말라.
이 문제는 그림 31.14에 나와 있다. 다섯 명의 "철학자"가 식탁 주위를 둘러앉았다. 총 다섯 개의 포크가 철학자와 철학자 사이에 하나씩 놓여 있다. 철학자는 식사하는 때가 있고 생각하는 때가 있다. 생각 중일 때는 포크가 필요 없다. 자신의 왼쪽과 오른쪽에 있는 포크를 들어야 식사를 할 수 있다. 이 포크를 잡기 위한 경쟁과 그에 따른 동기화 문제가 병행 프로그래밍에서 다루려는 식사하는 철학자 문제이다. 여기 각 철학자의 동작을 나타낸 기본 반복문이 있다.
while (1) {
think();
getforks();
eat();
putforks();
}
주요 쟁점은 getfork()와 putfork()의 루틴을 작성하되 교착 상태의 발생을 방지해야 하고, 어떤 철학자도 못 먹어서 굶주리면 안 되며 병행성이 높아야 한다 (즉, 가능한 많은 철학자가 동시에 식사를 할 수 있어야 한다).
Downey의 해법 [Dow08]과 같이 문제 해결을 위한 몇 가지 함수를 사용한다. 그 함수들은 다음과 같다.
int left(int p) { return p; }
int right(int p) { return (p + 1) % 5; }
철학자 p가 자신의 왼쪽에 있는 포크를 잡기 원한다면 left(p)를 호출한다. 마찬가지로 철학자 p가 자신의 오른쪽에 있는 포크를 잡기 원한다면 right(p)를 호출한다. 마지막 철학자(p=4)가 자신의 오른쪽의 포크인 포크 0을 잡으려고 할 경우를 위해서 나머지(modulo) 연산을 사용한다.
이 문제를 해결하기 위해서 세마포어가 필요하다. 각 포크마다 한 개씩 총 다섯 개가 있고 sem_t fork[5]로 정의한다.
불완전한 해답
이 문제를 해결하기 위한 첫 번째 시도를 해 보자. forks 배열에 있는 각 포크에 대한 세마포어를 1로 초기화를 하였고 각 철학자는 자신의 순번(p)을 알고 있다고 가정하자. 그림 31.15와 같이 getforks()와 putforks() 루틴을 작성할 수 있다.
void getforks() {
sem_wait(forks[left(p)]);
sem_wait(forks[right(p)]);
}
void putforks() {
sem_post(forks[left(p)]);
sem_post(forks[right(p)]);
}
그림 31.15 getforks()와 putforks() 루틴
이 (불완전한) 해답의 원리는 간단하다. 포크가 필요할 때 단순하게 하나의 "락"을 획득한다. 먼저 왼쪽의 것을 잡고 그 다음에 오른쪽의 것을 잡는다. 그리고 식사가 끝나면 잡은 순서대로 놓는다. 간단하지 않는가? 그래서 불완전하다는 것이다. 문제점이 보이는가? 생각해 보자.
문제는 교착 상태이다. 만약 각 철학자가 자신의 왼쪽의 포크를, 다른 철학자가 자신의 오른쪽의 포크를 잡기 전에 먼저 잡았다면, 각 철학자는 하나의 포크만 들고서 다른 하나의 포크를 잡을 수 있게 되기를 평생 기다리게 된다. 구체적으로 살펴보면, 철학자 0이 포크 0을 잡고, 철학자 1이 포크 1을 잡고, 철학자 2가 포크 2를, 철학자 3은 포크 3을, 그리고 철학자 4는 포크 4를 잡는다. 모든 포크는 다 누군가 잡고 있기 때문에 모든 철학자는 다른 철학자가 갖고 있는 포크를 기다리며 대기하게 된다. 교착 상태에 대해서는 곧 자세히 다룰 것이다. 우선 이 방법이 제대로 동작하는 해법이 아니라는 것만 알고 넘어가자.
해답: 의존성 제거
이 문제를 해결하기 위한 가장 간단한 방법은 최소한 하나의 철학자가 다른 순서로 포크를 집도록 하면 된다. 이 방법이 Dijkstra가 제시한 해결책이다. 가장 높은 순번의 철학자 4가 포크를 다른 순서로 획득한다고 가정하자. 그 순서에 대한 코드는 다음과 같다.
void getforks() {
if (p == 4) {
sem_wait(forks[right(p)]);
sem_wait(forks[left(p)]);
} else {
sem_wait(forks[left(p)]);
sem_wait(forks[right(p)]);
}
}
마지막 철학자가 오른쪽의 포크를 먼저 잡기 때문에 각 철학자가 하나의 포크를 든 채로 다른 포크를 기다리는 대기 상황은 발생하지 않는다. 환형 대기 상태가 끊어졌다. 이 해법에 대한 여러 상황을 한 번 생각해 보고, 동작한다는 것을 한 번 스스로 설득해 보라.
이와 비슷한 "유명한" 문제들이 더 있다. 예를 들어 흡연가의 문제 (Cigarette Smoker Problem)나 잠자는 이발사의 문제 (Sleeping Barber Problem)가 그것이다. 대부분이 병행성에 대한 연습 문제쯤 되지만, 이름 하나는 멋있다. 좀 더 알고 싶거나, 병행 프로그램 작성 연습을 하고 싶으면 참고하기 바란다 [Dow08].
31.7 세마포어 구현
마지막으로, 저수준 동기화 기법인 락과 컨디션 변수를 사용하여 우리만의 세마포어를 만들어 보자. 이른바 ... (기대하시라) ... 제마포어(Zemaphore)다. 이 작업은 그림 31.16에서 보인 것처럼 자명하다.
typedef struct _Zem_t {
int value;
pthread_cond_t cond;
pthread_mutex_t lock;
} Zem_t;
// 오직 하나의 쓰레드만 이 문장을 호출할 수 있음
void Zem_init(Zem_t *s, int value) {
s->value = value;
Cond_init(&s->cond);
Mutex_init(&s->lock);
}
void Zem_wait(Zem_t *s) {
Mutex_lock(&s->lock);
while (s->value <= 0)
Cond_wait(&s->cond, &s->lock);
s->value--;
Mutex_unlock(&s->lock);
}
void Zem_post(Zem_t *s) {
Mutex_lock(&s->lock);
s->value++;
Cond_signal(&s->cond);
Mutex_unlock(&s->lock);
}
그림 31.16 간단한 읽기-쓰기 락
팁 : 일반화를 주의하자 좋은 개념을 약간 확장하여 여러 부류의 문제를 해결할 수 있도록 하는 "일반화"라는 기법은 시스템 설계에 아주 유용하다. 하지만, 일반화를 할 때 주의해야 한다. Lampson이 경계한 것처럼 "일반화를 하지 말자. 일반적으로 일반화는 틀렸다." [Lam83]. 어떤 이는 세마포어를 락과 컨디션 변수의 일반화로 볼 수도 있다. 하지만, 그런 일반화가 필요하긴 한가? 그리고 세마포어를 이용하여 컨디션 변수를 구현하는 것이 어렵다는 것을 바탕으로 생각하면 이 일반화가 실제 당신이 생각하는 것만큼 일반적이지 않을 수도 있다.
그림에서 보는 것과 같이 하나의 락과 하나의 컨디션 변수를 사용하고 세마포어의 값을 나타내는 상태 변수 하나를 사용한다. 스스로 코드를 이해할 수 있을 때까지 공부해 보자. 지금!
Dijkstra가 정의한 세마포어와 여기서 정의한 제마포어 간의 중요한 차이 중 하나는 세마포어의 음수 값이 대기 중인 쓰레드의 수를 나타낸다는 부분이다. 사실 제마포어에서는 이 값이 0보다 작을 수가 없다. 이 방식이 구현하기도 쉽고 현재 Linux에 구현된 방식이기도 하다.
세마포어를 사용하여 락과 컨디션 변수를 만드는 것은 까다로운 문제이다. 병렬 연산에 많은 경험이 있는 개발자가 Windows 운영체제 환경에서 이것을 시도했지만 버그가 무척 많이 발생했다 [Bir04]. 한 번 스스로 시도해 보면, 세마포어를 사용하여 컨디션 변수를 구현하는 것이 생각보다 어렵다는 것을 알게 될 것이다. 한번 더 강조하지만, 정말 쉽지 않다. 세마포어로 컨디션 변수 구현에 성공한다면, 당신은 뛰어난 개발자의 소양을 갖고 있는 것이다.
31.8 요약
세마포어는 병행 프로그램 작성을 위한 강력하고 유연한 기법이다. 어떤 개발자들은 간단하고 유용하다는 이유 때문에 락과 컨디션 변수가 아닌 세마포어만을 사용하기도 한다.
이번 장에서는 몇 가지 고전적인 문제들과 그 해법에 대해서 다루었다. 더 알고 싶다면 참고할 만한 많은 자료들이 있다. 그 중 훌륭한 (거기다가 무료인) 책 중 하나는 Allen Downey의 것이다 [Dow08]. 이 책은 병행성에 대한 전반적인 내용과 세마포어에 대한 구체적인 이해를 돕기 위한 여러 퍼즐들을 다루고 있다. 진정한 병행성 전문가가 되는 것은 수년간의 노력이 필요한 일이다. 수업에서 배운 것 이상의 내용을 찾아서 공부하는 것이 이 주제를 정복하는 핵심 열쇠이다.
참고 문헌
[Bir04] "Implementing Condition Variables with Semaphores"
Andrew Birrell. December 2004. 컨디션 변수를 세마포어로 만드는 것이 얼마나 어려운지와 그리고 그 과정에서 저자들이 어떤 실수들을 했는지를 잘 보여주는 흥미 있는 글이다. 특히 관련이 있다고 보는 것은 이 그룹이 병렬 연산 프로그래밍을 수도 없이 많이 진행하였기 때문이다. Birrell의 경우 (다른 많은 것들 중에) 쓰레드 프로그래밍에 대한 가이드들의 저자로 유명하다.
[CB08] "Real-world Concurrency"
Bryan Cantrill and Jeff Bonwick. ACM Queue. Volume 6, No. 5. September 2008. 예전에 Sun이라는 회사에서 몇 명의 커널 해커들이 경험했던 병렬 연산 코드 관련한 문제들을 다룬 좋은 글이다.
[CHP71] "Concurrent Control with Readers and Writers"
P. J. Courtois, F. Heymans, and D. L. Parnas. Communications of the ACM, 14:10, October 1971. 읽기-쓰기 문제와 그에 대한 간단한 해법을 소개하였다. 이후의 저작에서는 좀 더 복잡한 해법을 제시했지만 여기서는 다루지 않았다. 너무 복잡하기 때문이다.
[Dij59] "A Note on Two Problems in Connexion with Graphs"
E. W. Dijkstra. Numerische Mathematik 1, 269–271, 1959. url: http://www-m3.ma.tum.de/twiki/pub/MN0506/WebHome/dijkstra.pdf. 1959년도에 알고리즘에 대해 연구했던 사람들이 있었다는 것이 믿겨지는가? 우리는 안 믿겨진다. 컴퓨터를 쉽게 다룰 수 있었던 시절도 아니었는데, 이 사람들은 세상을 변화시키는 것이라고 자각했던 것 같다.
[Dij68a] "Go-to Statement Considered Harmful"
E. W. Dijkstra. Communications of the ACM, volume 11(3): pages 147–148, March 1968. url: http://www.cs.utexas.edu/users/EWD/ewd02xx/EWD215.PDF. 소프트웨어 공학 분야의 시초라고도 여겨지는 글이다.
[Dij68b] "The Structure of the THE Multiprogramming System"
E. W. Dijkstra. Communications of the ACM, volume 11(5), pages 341–346, 1968. 컴퓨터 과학에 있어 시스템 작업은 지적 노동이라는 것이라는 것을 일깨워준 초기 논문들 중 하나이다. 계층적 시스템의 구성에서는 모듈 방식을 도입해야 한다고 강력하게 주장하였다.
[Dij71] "Hierarchical ordering of sequential processes"
E. W. Dijkstra. url: http://www.cs.utexas.edu/users/EWD/ewd03xx/EWD310.PDF. 식사하는 철학자를 포함하여 여러 병행성 문제들을 소개한다. 위키피디아에 소개된 이 문제도 상당히 유용한 정보를 담고 있다.
[Dij72] "Information Streams Sharing a Finite Buffer"
E. W. Dijkstra. Information Processing Letters 1: 179–180, 1972. url: http://www.cs.utexas.edu/users/EWD/ewd03xx/EWD329.PDF. Dijkstra가 모든 것을 발명했던가? 아니다. 하지만 그렇게 볼 수도 있다. 병렬 연산 코드에 어떤 것이 문제인지 명확하게 적었던 최초의 사람들 중의 하나이다. 하지만, 운영체제 설계의 전문가들은 Dijkstra가 설명한 문제들을 대부분 알고 있었던 것이 사실이기 때문에 너무 많은 업적을 Dijkstra의 것이라고 하는 것은 역사를 왜곡하는 것 같다.
[Dow08] "The Little Book of Semaphores"
A. B. Downey. url: http://greenteapress.com/semaphores/. 세마포어에 대한 좋은 (그리고 공짜!) 책이다. 이런 류를 좋아한다면 재미있는 문제들이 많이 있다.
[GR92] "Transaction Processing: Concepts and Techniques"
Jim Gray and Andreas Reuter. Morgan Kaufmann, September 1992. 특히 우리가 유머러스하게 받아들인 인용문은 해당 책의 485쪽에 있는 8.8절의 앞에 나와 있다. "1960년대에 개발된 첫 멀티프로세서는 Test-And-Set 명령어를 포함하고 있었다 ... 운영체제 개발자들이 적절한 알고리즘을 만들어 냈지만 몇 년의 시간이 흐른 후에 일반적으로 세마포어를 개발한 Dijkstra가 창시자라는 이름을 얻었다."
[Hil87] "Aspects of Cache Memory and Instruction Buffer Performance"
Mark D. Hill. Ph.D. Dissertation, UC Berkeley, 1987. 초기 시스템의 캐시에 집착하는 사람들을 위한 Hill의 학위 논문이다. 정량적 분석의 훌륭한 예가 되는 학위 논문이다.
[Lam83] "Hints for Computer Systems Design"
Butler Lampson. ACM Operating Systems Review, 15:5, October 1983. 유명한 시스템 연구가인 Lampson은 컴퓨터 시스템의 설계에 힌트를 사용하는 것을 사용했다. 힌트는 대체적으로 맞지만 틀릴 수도 있는 것이다. 그가 사용한 예에서는 대기 중인 쓰레드에게 기다리고 있던 값의 조건이 변경되었다고 signal()로 알려준다. 그렇지만 대기 중인 쓰레드가 깨어났을 때 이 조건이 참이라고 믿지 말라는 의미로 사용되었다. 시스템 설계를 위한 힌트를 다룬 이 논문에서 Lampson이 제안하는 일반론적인 힌트는 힌트를 사용해야 한다는 것이다. 들리는 것처럼 그렇게 복잡하지 않다.