제9장: 스케줄링: 비례 배분

스케줄링 : 비례 배분

이 장에서는 비례 배분(Proportional Share) 스케줄러, 혹은 공정 배분(fair share) 이라고도 하는 유형의 스케줄러에 대해 다루도록 하겠다. 비례 배분의 개념은 간단하다. 반환 시간이나 응답 시간을 최적화하는 대신 스케줄러가 각 작업에게 CPU의 일정 비율을 보장하는 것이 목적이다.

비례 배분 스케줄링의 좋은 예가 Waldspurger and Weihl [WW94]의 연구다. 추첨 스케줄링(lottery scheduling)으로 알려져 있다. 이 아이디어는 꽤 오래되었다 [KL98]. 기본 아이디어는 매우 간단하다. 다음 실행될 프로세스를 추첨을 통해 결정한다. 더 자주 수행되어야 하는 프로세스는 당첨 기회를 더 많이 준다. 쉽다. 아닌가? 이제 자세한 사항을 알아보자. 그러나 그 전에 핵심 문제를 살펴보자.

핵심 질문: 어떻게 CPU를 정해진 비율로 배분할 수 있는가

특정 비율로 CPU를 배분하는 스케줄러를 어떻게 설계할 수 있는가? 그렇게 하기 위한 중요한 기법은 무엇인가? 그 기법은 얼마나 효과적인가?

12.1 기본 개념: 추첨권이 당신의 몫을 나타낸다

추첨권(티켓)이라는 기본적인 개념이 추첨 스케줄링의 근간을 이룬다. 추첨권은 프로세스가 (또는 사용자 또는 그 무엇이든) 받아야 할 자원의 몫을 나타내는 데 사용된다. 프로세스가 소유한 티켓의 개수와 전체 티켓에 대한 비율이 자신의 몫을 나타낸다.

예를 살펴보자. A와 B 두 프로세스가 있다고 가정하자. A는 75장의 추첨권을, B 는 25장의 추첨권을 가지고 있다. A에게 75%의 CPU를, B에게 남은 25%를 할당하는 것이 목적이다.

추첨 스케줄링은 이러한 목적을 (타임 슬라이스가 끝날 때마다) 확률적으로 (하지만 결정적이지는 않게) 달성한다. 추첨 방식은 간단하다. 스케줄러는 전체 몇 장의 추첨권이 있는지 알아야만 한다 (우리의 예에서는 100장이다). 스케줄러는 추첨권을 선택한다. 제12장 스케줄링 : 비례 배분

무작위성의 이용

추첨권 스케줄링의 큰 장점 중 하나는 무작위성이다. 결정이 필요할 때, 이러한 무작위 방식은 강력하고 쉬운 방법이다.

무작위 방식은 전통적인 결정 방식에 비해 세 가지 장점이 있다. 첫째, 무작위 방식은 더 전통적인 방식이 잘 해결하지 못하는 특이 상황을 잘 대응한다. LRU 교체 정책을 생각해 보자 (가상 메모리의 나중 장에서 더 자세히 검토). LRU는 좋은 교체 알고리즘이지만 반복되는 순차적인 접근 패턴을 보이는 오버헤드에 대해서는 최악의 성능을 보인다. 반면, 무작위 방식에서는 그러한 최악의 경우가 발생하지 않는다.

둘째, 무작위 추첨 방식은 매우 가볍다. 관리해야 할 상태 정보가 거의 없기 때문이다. 전통적인 공정 배분 스케줄링 알고리즘에서는 각 프로세스가 사용한 CPU 양을 기록해야 한다. 이 정보는 각 프로세스를 실행시킬 때마다 갱신된다. 무작위 추첨 방식에서는 프로세스의 상태 정보만 필요하다 (예, 각 프로세스가 가진 추첨권의 개수).

마지막으로 무작위 추첨 방식은 매우 빠르다. 난수 발생 시간이 빠르기만 하면 결정 역시 빠르게 되고 따라서 속도가 요구되는 많은 경우에 사용될 수 있다. 물론, 속도를 증가시키기 위해서 추첨 과정을 덜 무작위 (pseudo-random)하게 만들기도 한다.

추첨권은 0 에서 99의 숫자다¹ . A가 0에서 74까지의 티켓을, B는 75에서 99까지의 추첨권을 가지고 있다. 뽑힌 추첨권 값에 따라 실행할 프로세스가 결정된다. 스케줄러는 당첨된 프로세스를 실행한다.

추첨 스케줄러의 당첨 추첨권의 예가 다음에 나와 있다.

63 85 70 39 76 17 29 41 36 39 10 99 68 83 63 62 43 0 49 49

그에 따른 스케줄링 결과는 다음과 같다.

A A A A A A A A A A A A A A A A B B B B

이 예에서 볼 수 있듯이 무작위성은 원하는 비율을 정확히 보장하지는 않는다. 앞의 예에서 B는 20개의 타임 슬라이스 중에 4개 타임 슬라이스를 (20%) 획득한다 (원래 목표인 25%가 아니라). 하지만, 두 작업이 장시간 실행될수록, 원하는 비율을 달성할 가능성이 높아진다.

12.2 추첨 기법

추첨권을 다루는 다양한 기법이 있다. 한 가지 기법은 **추첨권 화폐(ticket currency)**의 개념이다. 이 개념은 사용자가 추첨권을 자신의 화폐 가치로 추첨권을 자유롭게 할당할 수 있도록 허용한다. 시스템은 자동적으로 화폐 가치를 변환한다.

2 운영체제 : 아주 쉬운 세 가지 이야기 [V.0.90]

¹⁾ 컴퓨터 과학자들은 항상 0부터 세기 시작한다. 이 관습은 컴퓨터 전공자가 아닌 사람들에게는 매우 이상한 일로 받아들여지기 때문에 저명한 사람들은 항상 우리가 이렇게 하는 이유를 설명해야 한다는 의무감을 느껴 왔다 [Dij82].

몫을 표현하기 위한 추첨권의 사용

추첨 (그리고 보폭(stride)) 스케줄링의 설계에서 가장 기본적인 개념은 추첨권이다. 이 예에서는 추첨권이 CPU를 사용할 수 있는 프로세스의 몫을 나타내는 데 사용되고 있지만 훨씬 더 널리 적용될 수 있다. 예를 들어, 하이퍼바이저의 가상 메모리 관리에 관한 최근의 연구에서 Waldspurger는 게스트 운영체제의 메모리 할당 지분을 나타내는 데 추첨권이 어떻게 사용될 수 있는지 보여 준다 [Wal02]. 현재 소유 지분을 표현하기 위한 기법이 필요하다면 이 개념은 아마 ... (잠시 기다림) ... 추첨권일 것이다.

예를 들어, 사용자 A, B가 각각 100장의 추첨권을 받았다고 가정하자. 사용자 A는 A1과 A2의 두 개의 작업을 실행 중이고 자신이 정한 화폐로 각각 500장의 추첨권을 할당하였다(전체 1000장의 추첨권 중에). 사용자 B는 하나의 작업을 실행 중이고 자신의 기준 화폐 10장 중에 10장을 할당하였다. 시스템은 A1과 A2의 몫을 A의 기준 화폐 500장에서 전역 기준 화폐 각각 50장으로 변환한다. 마찬가지로, B1의 추첨권 10장은 추첨권 100장으로 변환된다. 전역 추첨권 화폐량 (총 200장) 기준으로 추첨한다.

User A \rightarrow 500 (A's currency) to A1 \rightarrow 50 (global currency) \rightarrow 500 (A's currency) to A2 \rightarrow 50 (global currency) User B \rightarrow 10 (B's currency) to B1 \rightarrow 100 (global currency)

다른 유용한 기법은 **추첨권 양도(ticket transfer)**이다. 양도를 통하여 프로세스는 일시적으로 추첨권을 다른 프로세스에게 넘겨줄 수 있다. 이 기능은 클라이언트/서버 환경에서 특히 유용하다. 클라이언트 프로세스는 서버에게 메시지를 보내 자신을 대신해 특정 작업을 해달라고 요청한다. 작업이 빨리 완료될 수 있도록 클라이언트는 서버에게 추첨권을 전달하고 서버가 자신의 요청을 수행하는 동안 서버의 성능을 극대화하려고 한다. 요청을 완수하면 서버는 추첨권을 다시 클라이언트에게 되돌려 주고 먼저와 같은 상황이 된다.

마지막으로, **추첨권 팽창(ticket inflation)**도 유용하게 사용된다. 이 기법에서 프로세스는 일시적으로 자신이 소유한 추첨권의 수를 늘이거나 줄일 수 있다. 물론 서로 신뢰하지 않는 프로세스들이 상호 경쟁하는 시나리오에서는 의미가 없다. 하나의 욕심 많은 프로세스가 매우 많은 양의 추첨권을 자신에게 할당하고 컴퓨터를 장악할 수 있다. 화폐 팽창 기법은 프로세스들이 서로 신뢰할 때 유용하다. 그런 경우 어떤 프로세스가 더 많은 CPU 시간을 필요로 한다면 시스템에게 이를 알리는 방법으로 다른 프로세스들과 통신하지 않고 혼자 추첨권의 가치를 상향 조정한다.

12.3 구현

추첨 스케줄링의 가장 큰 장점은 구현이 단순하다는 점이다. 필요한 것은 난수 발생기와 프로세스들의 집합을 표현하는 자료 구조(예, 리스트), 추첨권의 전체 개수 뿐이다.

리스트를 사용하여 프로세스를 관리한다고 가정하자. A, B 및 C 세 개의 프로세스로 구성되고 각자 몇 장의 추첨권을 가진다.

// counter: 당첨자를 발견했는지 추적하는 데 사용됨
int counter = 0;

// winner: 0부터 총 추첨권의 수 사이의 임의의 값을 얻기 위해
// 난수 발생기를 호출함
int winner = getrandom(0, totaltickets);

// current: 작업 목록을 탐색하는 데 사용
node_t *current = head;

// 티켓 값 > winner를 만족할 때까지 반복
while (current) {
    counter = counter + current->tickets;
    if (counter > winner)
        break; // 당첨자 발견
    current = current->next;
}
// "current"는 당첨자를 가리킴: 당첨자가 실행될 수 있도록 준비

〈그림 12.1〉 추첨 스케줄링 결정 코드

스케줄을 결정하기 위해 먼저 총 추첨권의 개수 $(400)^2$ 중에서 한 숫자를 선택해야 한다. 300이 선택되었다고 하자. 리스트를 순회하며 카운터 값을 이용하여 당첨자를 찾아낸다(그림 12.1).

프로세스 리스트를 순회하면서 counter의 값이 winner의 값을 초과할 때까지 각 추첨권 개수를 counter에 더한다. 값이 초과하게 되면 리스트의 현재 원소가 당첨자가 된다. 당첨 번호가 300인 우리의 예에서는 다음과 같이 진행된다. 먼저 A의 추첨권 개수가 더해져서 counter 값이 100으로 증가한다. 100은 300보다 작기 때문에 계속 루프를 실행한다. 다음 counter는 150(B의 추첨권 개수)으로 갱신되고, 아직 300보다 작기 때문에 다시 순회를 계속한다. 마침내 counter는 400(확실히 300보다 큼)으로 갱신되고 루프를 빠져 나오게 되고 current는 프로세스 C(당첨자)를 가리키게 된다.

일반적으로 리스트를 내림차순으로 정렬하면 이 과정이 가장 효율적이 된다. 정렬 순서는 알고리즘의 정확성에 영향을 주지는 않는다. 그러나 리스트를 정렬해 놓으면 검색 횟수가 최소화되는 것을 보장한다. 특히, 적은 수의 프로세스가 대부분의 추첨권을 소유하고 있는 경우에 효과적이다.

12.4 예제

추첨 스케줄링 동작을 쉽게 이해하기 위해서, CPU를 공유하는 두 개의 작업의 수행 시간을 살펴보자. 각 프로세스는 같은 개수의 추첨권(100)을 가지고 있으며 동일한 실행

²⁾ Björn Lindberg가 지적한 것처럼 놀랍게도 범위 안의 난수를 정확하게 선택하는 것 은 어려운 일이다. 자세한 내용은 http://stackoverflow.com/questions/2509679/ how-to-generate-a-random-number-from-within-a-range

시간을 갖는다 (R, 값을 변경할 수 있음).

우리는 두 작업을 거의 동시에 종료시키고자 한다. 그러나 추첨 스케줄링의 무작위성 때문에 한 작업이 다른 작업보다 먼저 종료될 수 있다. 이 차이를 정량화하기 위해, 간단한 불공정 지표(unfairness metric)인 U를 정의한다. U는 첫 번째 작업이 종료된 시간을 두 번째 작업이 종료된 시간으로 나눈 값이다. 예를 들어, R = 10, 첫 번째 작업은 시간 10에 종료했을 때 (그리고 두 번째 작업은 20에서 종료), U = 10/20 = 0.5. 두 작업이 거의 동시에 종료하면 U는 1에 근접해진다. 이 시나리오에서는 바로 그게 목표다. 완벽한 공정 스케줄러에서는 U = 1을 얻게 된다.

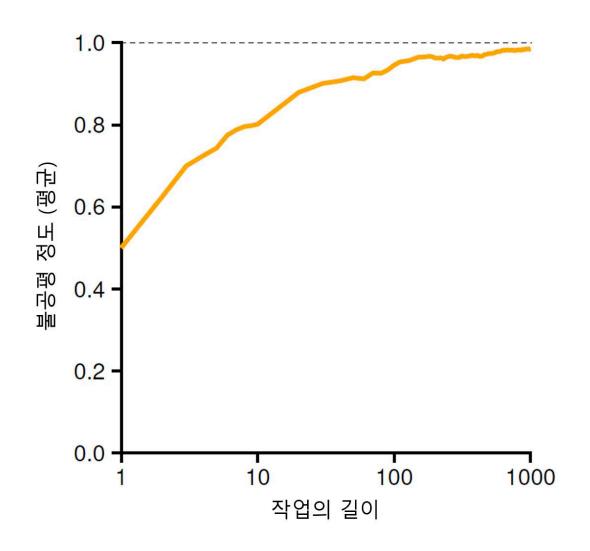
〈그림 12.2〉추첨권 배분 방식의 공정성 분석

그림 12.2은 평균적인 불공정 정도를 보이고 있다. 두 작업의 수행 시간은 1에서 1000까지 변경시켰으며 30번씩 실행시켰다. 결과는 이 장의 마지막에 제공되는 시뮬레이터를 통하여 생성되었다. 그래프에서 보듯 작업 길이가 길지 않은 경우, 평균 불공정 정도는 심각하다. 작업이 충분한 기간 동안 실행되어야 추첨 스케줄러는 원하는 결과에 가까워진다.

12.5 추첨권 배분 방식

추첨 스케줄링에서 아직 언급하지 않은 문제는 추첨권을 작업에게 나누어주는 방식이다. 작업들에게 추첨권을 몇 개씩 분배해야 하는가? 시스템 동작이 추첨권 할당 방식에 따라 크게 달라지기 때문에 상당히 어려운 문제이다. 한 가지 접근 방식은 사용자가 가장 잘 알고 있다고 가정하는 것이다. 각 사용자에게 추첨권을 나누어 준 후 사용자가 알아서 실행시키고자 하는 작업들에게 추첨권을 배분하는 것이다. 하지만 이건 해결책이 아니다. 어떤 일을 해야 하는지 전혀 제시하지 않는다. 주어진 작업 집합에 대한 "추첨권 할당 문제"는 여전히 미해결 상태다.

12.6 왜 결정론적(Deterministic) 방법을 사용하지 않는가

위에서 본 바와 같이, 무작위성을 이용하면 스케줄러를 단순하게(그러나 어느 정도 정확하게) 만들 수 있지만, 정확한 비율을 보장할 수 없다. 짧은 기간만 실행되는 경우는 더 그렇다. 이 때문에 Waldspurger는 결정론적 공정 배분 스케줄러인 보폭 스케줄링(stride scheduling) [Wal95]을 고안하였다.

보폭 스케줄링 역시 이해하기 쉽다. 시스템의 각 작업은 보폭을 가지고 있다. 보폭은 자신이 가지고 있는 추첨권 수에 반비례하는 값이다. 앞의 예에서 작업 A, B, C는 각각 100, 50, 250의 추첨권을 가지고 있으며 임의의 큰 값을 각자의 추첨권 개수로 나누어 보폭을 계산할 수 있다. 예를 들어 10,000을 각자의 추첨권 개수로 나누면 각 작업의 보폭은 100, 200 및 40이 된다. 이 값을 보폭(stride)이라고 부르며 프로세스가 실행될 때마다 pass라는 값을 보폭만큼 증가시켜 얼마나 CPU를 사용하였는지를 추적한다.

스케줄러는 보폭과 pass 값을 사용하여 어느 프로세스를 실행시킬지 결정한다. 기본적인 아이디어는 간단하다. 가장 작은 pass 값을 가진 프로세스를 선택한다. 프로세스를 실행시킬 때마다 pass 값을 보폭만큼씩 증가시킨다. Waldspurger [Wal95]가 작성한 의사코드는 아래와 같다:

current = remove_min(queue);      // pass 값이 최소인 클라이언트로 선택
schedule(current);                // 자원을 타임 퀀텀만큼 선택된 프로세스에게 할당
current->pass += current->stride; // 다음 pass 값을 보폭 값을 이용하여 갱신
insert(queue, current);           // 다시 큐에 저장한다

세 작업(A, B, C), 각자의 보폭은 각각 100, 200, 40이다. 각자의 pass 값은 모두 0에서 시작한다. 처음에는 pass 값이 같기 때문에 아무 프로세스나 실행될 수 있다. A를 선택했다고 가정하자(임의로, 값이 제일 작은 프로세스 중에서 아무거나). A가 실행된다. 타임 슬라이스만큼 실행되고 종료될 때 pass 값을 100으로 갱신한다. 다음에 B가 실행되고 해당 pass 값이 200으로 갱신된다. 마지막으로 C를 실행하고, pass 값은 40으로 갱신된다. 이 시점에서 알고리즘은 가장 작은 pass 값을 가진 C를 선택하고 80으로 갱신한다(C의 보폭은 40이다). 다음 C가 다시 실행되고 (아직 최소 pass 값) 120으로 갱신된다. 이제 A가 실행되고 200으로 갱신된다(이제 B와 같아진다). 다음 C가 두 번 더 실행되고 pass 값은 160을 거쳐 200으로 갱신된다. 이 시점에서 모든 pass 값은 다시 같아지게 되고 이런 선택 과정이 계속 반복된다. 그림 12.3에 스케줄러의 동작이 나와 있다.

그림에서 알 수 있듯이, C는 5번, A는 2번, B는 한 번만 실행되었다. 이 횟수는 각자 가진 추첨권의 개수 250, 100, 50과 정확히 비례한다. 추첨 스케줄링은 정해진 비율에 따라 확률적으로 CPU를 배분한다. 보폭 스케줄링은 각 스케줄링 주기마다 정확한 비율로 CPU를 배분한다.

그렇다면 이런 질문을 던질지 모른다. 보폭 스케줄링의 정확도를 고려할 때, 추첨 스케줄링을 왜 사용하는가? 추첨 스케줄링은 보폭 스케줄링이 가지고 있지 않은 멋진 특성을 가지고 있다. 상태 정보가 필요 없다. 위 보폭 스케줄링의 예에서 스케줄링 중간에 새로운 작업이 시스템에 도착했다고 상상해 보자. pass 값은 얼마가 되어야 하는가? 0으로 지정되어야 하는가? 그렇다면 CPU를 독점하게 될 것이다. 추첨 스케줄링에서는

0	0	0	A
100	0	0	B
100	200	0	C
100	200	40	C
100	200	80	C
100	200	120	A
200	200	120	C
200	200	160	C
200	200	200

〈그림 12.3〉보폭 스케줄링 : 추적

프로세스 상태 (CPU 사용 현황, pass 값)를 유지할 필요가 없다. 새 프로세스를 추가할 때, 새로운 프로세스가 가진 추첨권의 개수, 전체 추첨권의 개수만 갱신하고 스케줄한다. 이런 이유로 추첨 스케줄링에서는 새 프로세스를 쉽게 추가할 수 있다.

12.7 요약

우리는 비례 배분 스케줄링의 개념을 소개하고, 추첨권 및 보폭 스케줄링이라는 두 가지 구현 방식에 대해 간단하게 논의하였다. 추첨권 스케줄링은 무작위성(randomness)을 사용한다. 보폭 스케줄링은 같은 목적을 결정적 방법으로 달성한다. 둘 다 개념적으로 흥미롭지만 여러 이유로 CPU 스케줄러로서 널리 사용되고 있지 않다. 한 가지 이유는 이러한 접근 방식이 특히 입출력과 맞물렸을 때, 제대로 동작하지 않는다는 것이다 [AC97]. 또 다른 이유는 추첨권 할당이라는 어려운 문제가 미해결 상태로 남아 있다는 것이다. 즉, 브라우저에 얼마나 추첨권을 할당해야 하는가? 범용 스케줄러 (앞서 언급한 MLFQ 그리고 다른 유사 Linux 스케줄러 같은)는 그러한 문제를 더 직관적으로 해결하고, 때문에 더 널리 사용되고 있다.

비례 배분 스케줄러는 추첨권 할당량을 비교적 정확하게 결정할 수 있는 환경에서 유용하게 사용된다. 예를 들어, 가상화 데이터 센터에서 Windows 가상 머신에 CPU 사이클의 1/4을 할당하고 나머지는 Linux 시스템에 할당하고 싶은 경우 비례 배분이 간단하고 효과적이다. 이러한 기법이 VMware ESX 서버에서 메모리를 비례 배분하는 데 어떻게 사용되는지를 알고 싶으면 Waldspurger [Wal02]를 참조하시오.

참고 문헌

[AC97] "Extending Proportional-Share Scheduling to a Network of Workstations"

Andrea C. Arpaci-Dusseau and David E. Culler

PDPTA'97, June 1997

클러스터 환경에서 더 잘 동작하도록 비례 배분 스케줄링을 확장하는 방법에 대한 본 저자 중 하나의 논문.

[Dij82] "Why Numbering Should Start At Zero"

Edsger Dijkstra

url: http://www.cs.utexas.edu/users/EWD/ewd08xx/EWD831.PDF

컴퓨터 과학의 선구자 중 한 사람인 E. Dijkstra의 짧은 메모. 책의 행성 섹션에서 이 사람에 대해 더 많이 읽게 될 것이다. 한 번 이 노트를 읽기도록. 이 노트는 다음과 같은 인용을 포함한다. "내 동료 중 한 사람이—컴퓨터 과학자가 아닌—은 컴퓨터 과학자들을 현학적이라고 비난하였다. 이들이 숫자를 0부터 센다는 것이 비난의 이유였다." 이 노트는 0부터 세는 것이 논리적인 이유에 대해 설명한다.

[KL98] "A Fair Share Scheduler"

J. Kay and P. Lauder

CACM, Volume 31 Issue 1, January 1988

공정 배분 스케줄러에 대한 초기 참고 문헌.

[Wal95] "Lottery and Stride Scheduling: Flexible Proportional-Share Resource Management"

Carl A. Waldspurger

Ph.D. Thesis, MIT, 1995

추첨권과 보폭 스케줄링의 개요를 설명하는 Waldspurger의 수상 논문. 언젠가 박사 학위 논문을 쓸 생각이 있다면 주위에 좋은 본보기를 가지고 있어야 한다. 바로 이 논문이 그러한 좋은 본보기이다.

[Wal02] "Memory Resource Management in VMware ESX Server"

Carl A. Waldspurger

OSDI '02, Boston, Massachusetts

VMM (일명 hypervisor)에서의 메모리 관리에 관한 논문. 읽기 쉬울 뿐 아니라 논문에는 이 새로운 VMM-단계의 메모리 관리에 관한 수많은 멋진 아이디어가 포함되어 있다.

[WW94]"Lottery Scheduling: Flexible Proportional-Share Resource Management" Carl A. Waldspurger and William E. Weihl

OSDI '94, November 1994

추첨 스케줄링에 관한 획기적인 논문. 이 논문은 시스템 커뮤니티가 스케줄링, 공정 배분 및 단순 무작위 알고리즘의 힘에 관한 연구를 다시 할 수 있도록 활력을 불어넣었다.

숙제

lottery.py 프로그램은 추첨 스케줄러의 동작을 살펴볼 수 있게 한다. 자세한 사항은 README를 참조하시오.

문제

• 1. 3개의 작업 및 1, 2, 3의 랜덤 시드를 위한 시뮬레이션을 위한 해결책을 계산하시오.
• 2. 다음 두 가지 특정 작업을 실행시켜 보라. 각 작업의 길이는 10, 작업 0은 1장의 추첨권, 작업 1은 100장의 추첨권을 가진다 (예, -l 10:1,10:100). 추첨권의 개수가 심하게 불균형을 이룰 경우 어떻게 동작하나? 작업 0은 작업 1이 종료하기 전에 실행될 수 있는가? 얼마나 자주 실행될 것인가? 일반적으로 이러한 추첨권의 불균형은 추첨 스케줄링의 동작에 어떤 영향을 미치는가?
• 3. 작업의 길이가 100이고 100장의 같은 추첨권을 가진 두 작업 (-l 100:100,100:100)을 실행시킨다면 스케줄러는 얼마나 불공정한가? (확률적인) 답을 결정하기 위해 몇몇 다른 랜덤 시드를 가지고 실행해 보시오. 불공정성은 하나의 작업이 다른 작업보다 얼마나 일찍 종료하느냐를 기준으로 결정된다고 하자.
• 4. 타임 퀀텀의 크기 (-q)가 커질수록 이전 질문에 대한 대답은 어떻게 바뀔까?
• 5. 이 장에서 나온 것 같은 그래프를 만들 수 있는가? 탐구해 볼만한 다른 것은 무엇인가? 보폭 스케줄러의 그래프는 어떻게 될까?