제17장: 빈 공간 관리

이 장에서는 메모리 가상화 논의에서 약간 우회하여 모든 메모리 관리 시스템의 근본적인 측면을 논의한다. 여기서 메모리 관리 시스템이란 프로세스 힙의 페이지를 관리하는 malloc 라이브러리일 수도 있고 혹은 프로세스의 주소 공간의 일부분을 관리하는 운영체제 자체일 수도 있다. 구체적으로, 빈 공간 관리에 관련된 문제를 논의할 것이다.

문제를 구체화해 보자. 페이징 개념을 논의할 때 보겠지만 빈 공간 관리는 쉬울 수 있다. 관리하고 있는 공간이 고정 크기의 단위로 나누어져 있는 경우 특히 쉽다. 그런 경우 그냥 이 고정 크기 단위의 리스트를 유지하면 된다. 클라이언트가 그 중 하나를 요청하면 첫 번째 항목을 반환하면 된다.

빈 공간 관리가 더 어렵고 흥미로운 경우는 관리하는 공간이 가변 크기 빈 공간들의 집합으로 구성되어 있는 경우이다. 이 경우는 malloc()과 free()에서처럼 사용자 수준 메모리 할당 라이브러리에서, 그리고 세그멘테이션으로 물리 메모리를 관리하는 운영체제에서 발생한다. 어느 경우에도 외부 단편화가 존재한다. 빈 공간은 다양한 크기의 작은 조각으로 분할되어 결국 단편화된다. 빈 공간들의 전체 크기가 요청된 것보다 크더라도 하나의 연속된 영역이 존재하지 않으면 요청은 실패할 수 있다.

	미사용	사용 중	미사용
0	1	10 2	20 3	0

그림은 이러한 문제의 예를 보여 준다. 이 경우 빈 공간의 전체 크기는 20바이트이다. 불행히도, 10바이트 짜리 두 조각으로 나누어져 있다. 그 결과, 20바이트의 빈 공간이 있지만 15바이트의 요청은 실패한다. 이것이 이 장에서 해결하고자 하는 문제이다.

핵심 질문: 빈 공간을 어떻게 관리하는가

가변 크기의 요구를 충족시켜야 할 때, 빈 공간은 어떻게 관리되어야 하는가? 단편화를 최소화하기 위해 어떤 전략을 사용할 수 있는가? 여러 대안들의 시간과 공간의 오버헤드는 어떻게 되는가?

17.1 가정

이 논의의 대부분은 사용자 수준 메모리 할당 라이브러리에 존재하는 메모리 할당기의 발전 역사에 초점을 맞출 것이다. 이 내용들은 Wilson의 저서에 잘 정리되어 있다 [RWi+95]. 더 자세한 사항을 알려면 원본 문서를 읽어 보기 바란다¹.

malloc()과 free()에서 제공하는 것과 같은 기본 인터페이스를 가정한다. 구체적으로 void *malloc(size_t size)는 응용 프로그램이 요청한 바이트 수를 나타내는 변수 size를 인자로 받아들인다. 이 함수는 요청된 크기와 같거나 큰 영역을 가리키는, 타입이 없는 또는 C 언어의 용어로 void 포인터를 반환한다. 대응되는 루틴 void free(void *ptr)는 포인터를 인자로 전달하고 해당 영역을 해제한다. 인터페이스의 의미에 주의하라. 공간을 해제할 때 사용자는 라이브러리에게 크기 정보를 전달하지 않는다. 라이브러리는 포인터만으로 해제하고자 하는 메모리 영역의 크기를 파악해야 한다. 크기를 알아내는 방법에 대해 나중에 논의할 것이다.

이 라이브러리가 관리하는 공간은 역사적으로 힙(heap)으로 불리며, 힙의 빈 공간을 관리하는 데는 일반적인 링크드리스트가 사용된다. 이 자료 구조는 영역 내의 모든 빈 청크에 대한 주소를 갖고 있다. 물론, 이 자료 구조는 반드시 리스트일 필요는 없고 빈 공간들을 표현할 수 있는 자료 구조면 충분하다.

우리는 위에서 언급한 것처럼 외부 단편화 방지에 특히 중점을 두겠다. 물론, 내부 단편화 문제도 있을 수 있다. 할당기가 요청한 크기보다 더 큰 메모리 청크를 할당할 경우, 요청되지 않은 사용되지 않는 공간에 대해서는 할당 청크의 내부에서 낭비가 일어났기 때문에 내부 단편화라고 간주된다. 할당 공간 낭비의 또 다른 예라고 할 수 있다. 논의를 단순화하기 위하여, 그리고 두 유형 중 더 흥미롭기 때문에 외부 단편화에 초점을 맞출 것이다.

우리는 또한 클라이언트에게 할당된 메모리는 다른 위치로 재배치될 수 없다고 가정한다. 예를 들어, 프로그램이 malloc()을 호출하여 힙의 일부 영역에 대한 포인터를 받으면, 그 메모리 영역은 대응하는 free()를 통하여 반환될 때까지 프로그램이 소유하게 되고 라이브러리에 의해 다른 위치로 옮겨질 수 없다. 단편화 해결에 유용하게 사용되는 빈 공간의 압축은 이 경우에는 사용이 불가능하다². 운영체제가 세그멘트를 구현할 때는 단편화를 해결하기 위하여 압축을 사용할 수 있다. 이에 대해서는 세그멘테이션에 관해 논의한 장에서 언급하였다.

17.2 저수준 기법들

세부 정책에 대해 자세히 설명하기 전에 먼저 대부분의 할당기에서 사용되는 일반적인 기법에 대해 논의한다. 첫 번째로 분할(splitting)과 병합(coalescing)의 기초에 대해서 알아본다. 두 번째로 할당된 영역의 크기를 빠르고 상대적으로 쉽게 파악할 수 있는 방법을 설명한다. 마지막으로, 빈 공간과 사용 중인 공간을 추적하기 위해 빈 공간 내에 간단한 리스트를 구현하는 방법에 대해 설명할 것이다.

분할과 병합

빈 공간 리스트는 힙에 있는 빈 공간들의 집합이다. 30바이트의 힙이 있다고 가정하자.

	미사용	사용 중		미사용
0	1	10	20		30

이 힙의 빈 공간 리스트에는 2개의 원소가 있다. 하나는 첫 번째 10바이트의 빈 세그멘트(바이트 0-9)를 설명하고 다른 하나는 나머지 빈 세그멘트(바이트 20-29)를 표현한다.

앞에서 언급한 바와 같이, 10바이트를 초과하는 모든 요청은 실패하여 NULL을 반환할 것이다. 요청한 크기에 해당하는 메모리 청크가 없기 때문이다. 10바이트에 대한 요청은 둘 중 하나의 빈 청크를 사용하여 쉽게 충족된다. 그러나 10바이트보다 적은 요청에 대해서는 어떤 일이 일어날까?

메모리를 1바이트만 요청했다고 가정하자. 이 경우 할당기는 분할(splitting)로 알려진 작업을 수행한다. 요청을 만족시킬 수 있는 빈 청크를 찾아 이를 둘로 분할한다. 첫 번째 청크는 호출자에게 반환되고, 두 번째 청크는 리스트에 남게 된다. 따라서 위의 예에서 1바이트 요청이 발생하고 할당기가 리스트의 두 번째 원소를 사용하여 요청을 충족시키기로 했다고 가정하자. malloc()은 20(1바이트가 할당된 영역의 주소)을 반환하고 최종 빈 리스트는 다음과 같이 될 것이다.

기본적인 리스트의 모습은 바뀌지 않았다는 것을 알 수 있다. 유일한 변경 사항은 빈 공간이 이제 20이 아니라 21에서 시작한다는 것과 빈 공간의 길이가 이제 9라는 것이다². 요청이 특정 빈 청크의 크기보다 작은 경우 분할 기법을 사용한다.

분할에 당연히 동반되는 기법은 빈 공간의 병합(coalescing)이다. 위의 예를 다시 한 번 보자 (빈 공간 10바이트, 사용 중 10바이트, 또 하나의 빈 공간 10바이트).

응용 프로그램이 free(10)을 호출하여 힙의 중간에 존재하는 공간을 반환할 때 어떤 일이 일어나는가? 깊게 생각하지 않고 이 빈 공간을 다시 리스트에 추가할 경우 다음과 같은 모양이 될 것이다.

무슨 문제가 있는지 살펴보자. 자 이제 힙 전체가 비어 있지만, 10바이트 길이의 청크 3개로 나누어져 있다. 사용자가 20바이트를 요청하는 경우 단순한 리스트 탐색은 그와 같은 빈 청크를 발견하지 못하고 실패를 반환한다.

할당기가 이 문제를 방지하기 위하여 할 수 있는 일은 메모리 청크가 반환될 때 빈 공간들을 병합하는 것이다. 아이디어는 간단하다 : 메모리 청크를 반환할 때 해제되는 청크의 주소와 바로 인접한 빈 청크의 주소를 살펴본다. 새로 해제된 빈 공간이 왼쪽의 빈 청크와 바로 인접해 있다면 (혹은 이 예에서처럼 양쪽으로) 그들을 하나의 더 큰 빈 청크로 병합한다. 병합 이후의 최종 리스트는 다음과 같은 모양이 될 것이다.

이 상태는 할당이 한 번도 일어나지 않은 최초의 힙 리스트의 모양이다. 병합 기법을 사용하여 할당기가 커다란 빈 공간을 응용 프로그램에게 제공할 수 있다는 것을 더 보장할 수 있다.

할당된 공간의 크기 파악

free(void *ptr) 인터페이스는 크기를 매개변수로 받지 않는다는 것을 알고 있을 것이다. 포인터가 인자로 전달되면 malloc 라이브러리는 해제되는 메모리 영역의 크기를 신속히 파악하여 그 공간을 빈 공간 리스트에 추가시킬 수 있다고 가정한다.

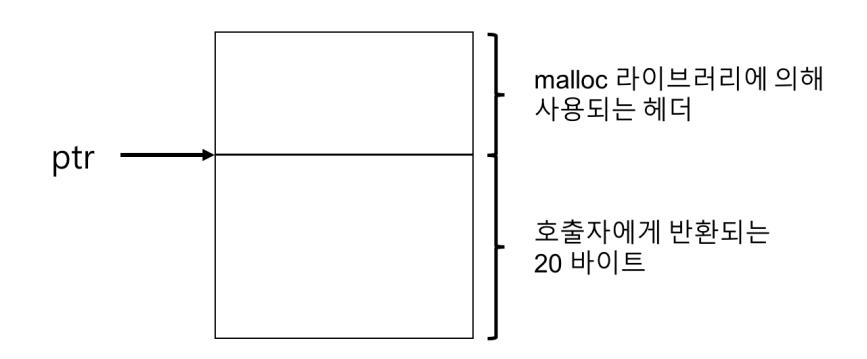
이 작업을 위해 대부분의 할당기는 추가 정보를 헤더(header) 블럭에 저장한다. 헤더 블럭은 메모리에 유지되며 보통 해제된 청크 바로 직전에 위치한다. 예를 살펴보자(그림 20.1). 이 예에서는 ptr이 가리키는 크기 20바이트의 할당된 블럭을 검토하고

³⁾ 이 논의는 헤더가 없다고 가정한다. 비현실적인 가정이지만 당분간 논의를 간단하게 하기 위해 가정한다.

⟨그림 20.1⟩ 할당된 영역과 헤더

$\langle$ 그림 $20.2\rangle$ 특정 값이 저장된 헤더

있다. 사용자는 malloc()을 호출하고 그 결과를 ptr에 저장하였다고 가정하자. 예를 들어, ptr = malloc(20);

헤더는 적어도 할당된 공간의 크기는 저장해야 한다(이 경우 20). 또한, 해제 속도를 향상시키기 위한 추가의 포인터, 부가적인 무결성 검사를 제공하기 위한 매직 넘버, 및 기타 정보를 저장할 수 있다. 다음과 같이 할당 영역의 크기와 매직 넘버를 저장하는 간단한 헤더를 가정하자.

typedef struct __header_t {
   int size;
   int magic;
} header_t;

위의 예제는 그림 17.2에서 볼 수 있는 것과 비슷하다. 사용자가 free(ptr)을 호출하면 라이브러리는 헤더의 시작 위치를 파악하기 위해 간단한 포인터 연산을 한다.

void free(void *ptr) {
   header_t *hptr = (void *)ptr - sizeof(header_t);
   ...

헤더를 가리키는 포인터를 얻어 내면, 라이브러리는 매직 넘버가 기대하는 값과 일치하는지 비교하여 건전성 검사(sanity check)를 실시한다(assert(hptr->magic == 1234567)). 그리고 새로 해제된 영역의 크기를 간단한 수학을 통해 계산한다(즉, 헤더의 크기를 영역의 크기에 더함). 주의할 점이 있다. 빈 영역의 크기는 헤더 크기 더하기 사용자에게 할당된 영역의 크기가 된다. 사용자가 $N$ 바이트의 메모리 청크를 요청하면 라이브러리는 크기 $N$의 빈 청크를 찾는 것이 아니라 빈 청크의 크기 $N$ 더하기 헤더의 크기인 청크를 탐색한다.

빈 공간 리스트 내장

지금까지 우리는 간단한 빈 공간 리스트의 개념만을 다루었다. 이러한 리스트를 빈 공간에 어떻게 구현할 수 있는가?

보통 새로운 노드를 위한 공간이 필요할 때 malloc()을 호출한다. 불행하게도 메모리 할당 라이브러리 루틴에서는 이것이 불가능하다. 대신 빈 공간 내에 리스트를 구축해야 한다

4096바이트 크기의 메모리 청크가 있다고 하자. 즉, 힙의 크기는 4KB이다. 이를 빈 공간 리스트로 관리하기 위해서 먼저 리스트를 초기화해야 한다. 처음에 리스트는 4096(빼기 헤더 크기) 길이의 항목 하나를 가지고 있다. 이 리스트 노드의 설명은 다음과 같다.

typedef struct __node_t {
    int size;
    struct __node_t *next;
} node_t;

힙을 초기화하고 힙에 빈 공간 리스트의 첫 번째 원소를 넣는 코드를 살펴보자. 힙은 시스템 콜 mmap()을 호출하여 얻어진 영역에 구축된다고 가정한다. 이 방법이 힙을 구축하기 위한 유일한 방법은 아니지만, 이 예에서는 충분하다. 코드는 다음과 같다.

// mmap()이 빈 공간의 청크에 대한 포인터를 반환
node_t *head = mmap(NULL, 4096, PROT_READ|PROT_WRITE,

이 코드의 실행 후 리스트는 크기 4088의 항목 하나만을 가지게 된다. 매우 작은 힙이지만, 우리의 논의를 위해서는 충분하다. head 포인터는 이 영역의 시작 주소를 담고 있다. 영역의 시작 주소를 16 KB라고 가정하자(아무 가상 주소라도 상관 없다). 이때 힙의 모양은 그림 17.3에서 보는 것과 비슷할 것이다.

자, 이제 100바이트 메모리 청크가 요청되었다고 생각해 보자. 이 요청을 처리하기 위해 라이브러리는 먼저 충분한 크기의 청크를 찾는다. 하나의 빈 청크(크기: 4088) 만이 존재하기 때문에 이 청크가 선택된다. 요청을 처리하기에 충분히 큰 크기, 앞서 말한 것처럼 빈 영역의 크기 더하기 헤더의 크기를 충족시킬 수 있는 청크와 나머지 빈 청크 두 개로 분할한다. 헤더의 크기를 8바이트라고 가정하면(정수형의 크기와 정수형의 매직 넘버), 이제 힙의 공간의 모습은 그림 17.4에 보이는 것과 비슷할 것이다.

100바이트에 대한 요청이 오면 라이브러리는 기존 하나의 빈 청크 중 108바이트를 할당하고 할당 영역을 가리키는 포인터(그림의 ptr)를 반환한다. 그리고 나중에 free()에서 사용할 수 있도록 할당된 공간 직전 8바이트에 헤더 정보를 넣는다. 그런 후 하나 남은 빈 노드를 3980바이트 (4088-108)로 축소한다.

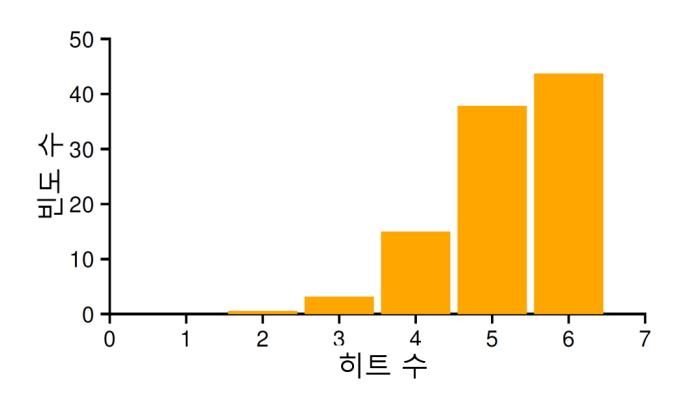
그림 17.3 하나의 빈 청크만을 가진 힙

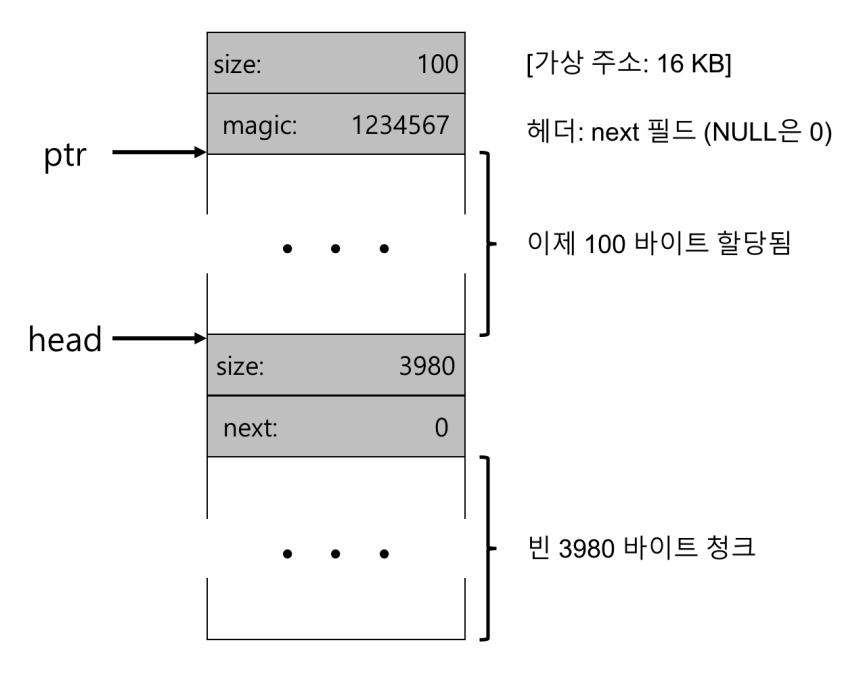
그림 17.4 힙: 한 번의 할당 후

자, 이제 100바이트씩 (또는 헤더 포함 108바이트) 할당된 3개의 공간이 존재하는 힙을 살펴보자. 이 힙의 모습이 그림 17.5와 같다.

그림에서 볼 수 있듯이 힙의 시작 부분 324바이트가 현재 할당되어 있다. 3개의 헤더와 호출 프로그램에 의해 사용 중인 3개의 100바이트 영역을 볼 수 있다. 빈 공간 리스트는 여전히 head가 가리키는 하나의 노드로 구성되어 있지만 세 번의 분할 이후 3764바이트로 축소된 모습이다. 프로그램이 free()를 통해 일부 메모리를 반환하면 어떤 일이 벌어질까?

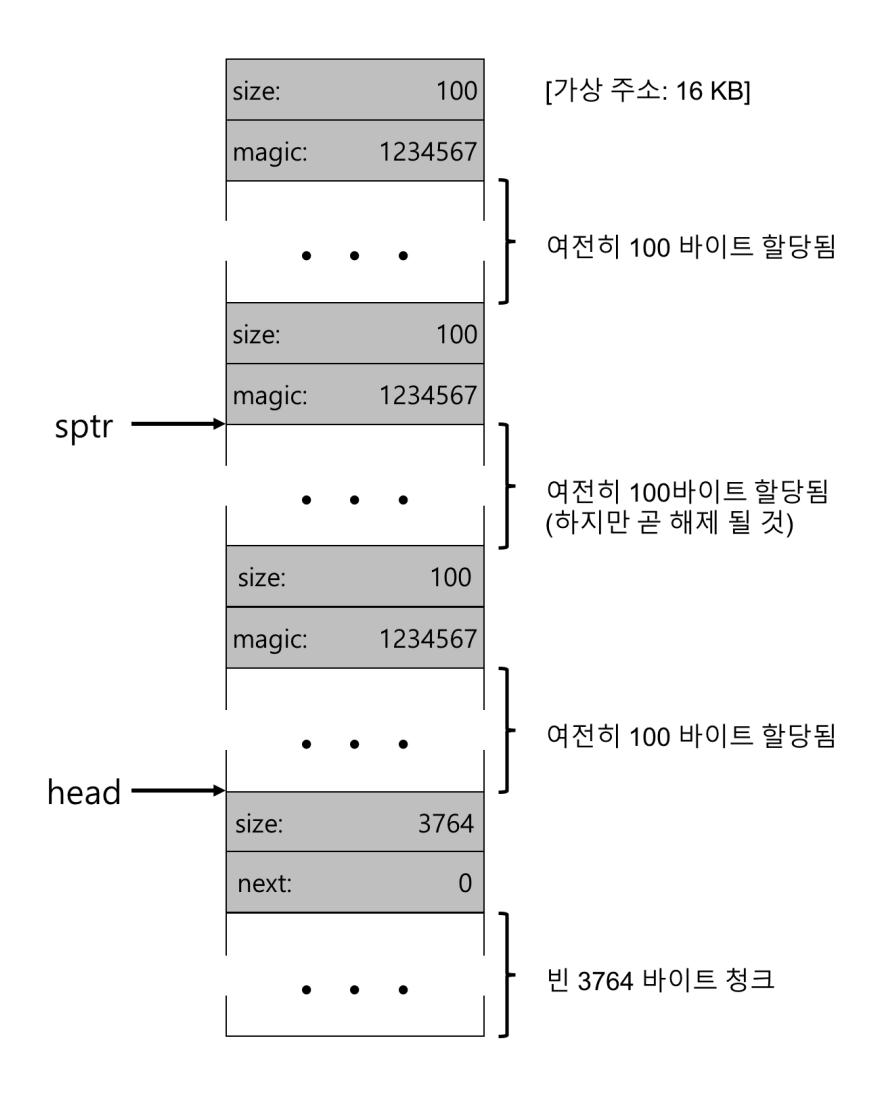
그림 17.5 3개의 할당 청크를 가진 빈 공간

이 예제에서 응용 프로그램은 free(16500)을 호출하여 할당 영역 중 가운데 청크를 반환한다. 16500은 메모리 영역의 시작 주소 16384, 이전 메모리 청크의 크기 108, 해제되는 청크의 헤더 8바이트를 모두 더해서 나온 값이다. 그림에서 이 값은 sptr이 가리킨다.

라이브러리는 신속히 빈 공간의 크기를 파악하고, 빈 청크를 빈 공간 리스트에 삽입한다. 빈 공간 리스트의 헤드 쪽에 삽입한다고 가정하면 공간의 모양은 그림 17.6과 같다.

이제 빈 공간 리스트의 첫 번째 원소는 작은 빈 청크(100바이트 크기이며 리스트의 헤드가 가리킴)이고 두 번째 원소는 큰 빈 청크(3764바이트)이다. 드디어 우리 리스트가 하나 이상의 원소를 가진다! 불행하지만 흔히 일어나는 단편화가 발생하였다.

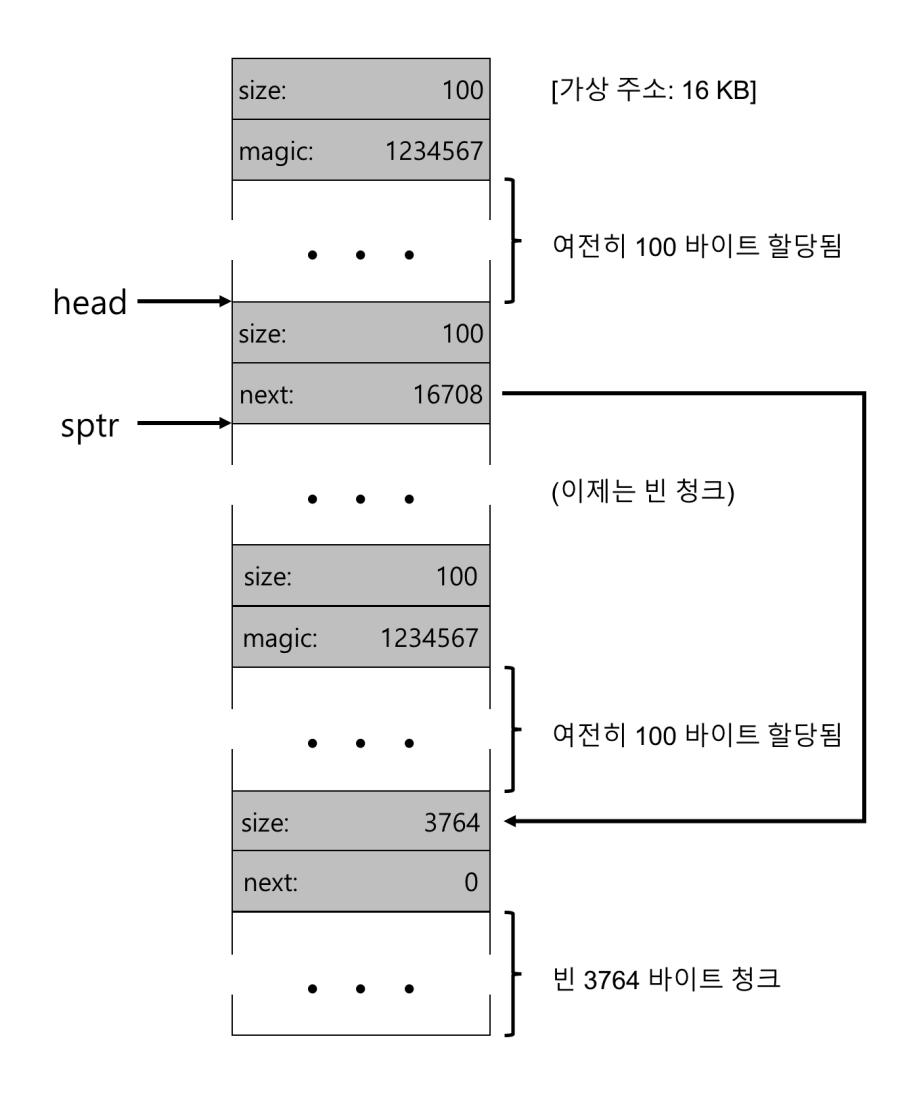
그림 17.6 2개의 할당 청크를 가진 빈 공간

마지막으로 나머지 2개의 사용 중인 청크가 해제된다고 하자. 병합이 없다면, 작은 단편으로 이루어진 빈 공간 리스트가 될 것이다(그림 17.7 참조).

그림에서 볼 수 있듯이, 우리는 지금 큰 난관에 봉착했다. 왜? 우리는 리스트를 병합하지 않았다. 모든 메모리가 비어 있긴 하지만, 전부 조각나 있기 때문에 한 청크가 아니라 단편으로 이루어진 메모리처럼 보인다. 해결책은 간단하다: 리스트를 순회하면서 인접한 청크를 병합하면 된다. 병합이 완료되면 힙은 전체 하나의 큰 청크가 된다.

힙의 확장

이제 마지막 주제를 다루도록 하겠다. 힙 공간이 부족한 경우에 어떻게 할 것인가? 가장 쉬운 방법은 단순히 실패를 반환하는 것이다. 어떤 경우에는 이 방법이 유일한 대안이며,

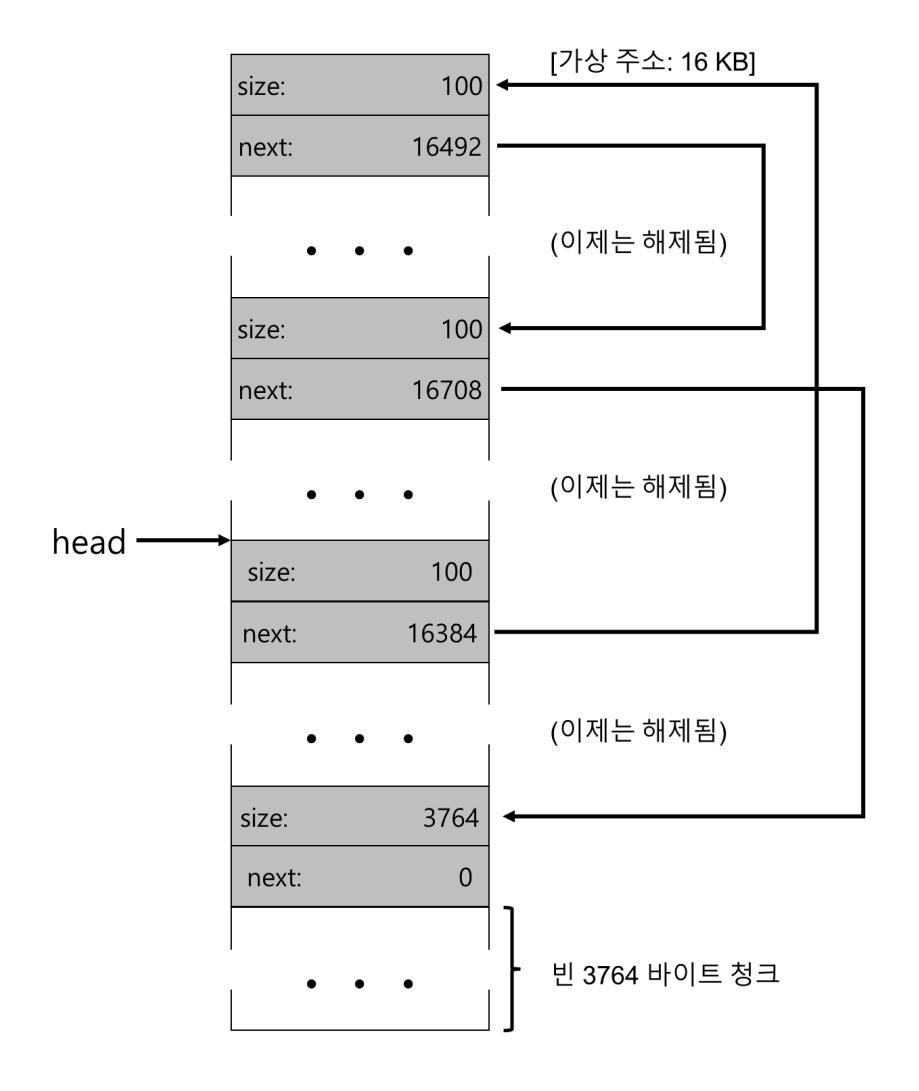
그림 17.7 병합되지 않은 빈 공간 리스트

따라서 NULL을 반환하는 것은 훌륭한 접근법이다. 너무 낙담하지 마라! 당신은 노력했고 실패했지만 잘 싸운거다.

대부분의 전통적인 할당기는 적은 크기의 힙으로 시작하여 모두 소진하면 운영체제로부터 더 많은 메모리를 요청한다. 할당기는 힙을 확장하기 위하여 특정 시스템 콜 (예, 대부분의 Unix 시스템에서는 sbrk)을 호출한다. 그런 후 확장된 영역에서 새로운 청크를 할당한다. sbrk 요청을 수행하기 위해 운영체제는 빈 물리 페이지를 찾아 요청 프로세스의 주소 공간에 매핑한 후, 새로운 힙의 마지막 주소를 반환한다. 이제부터 더 큰 힙을 사용할 수 있고 요청은 성공적으로 충족될 수 있다.

17.3 기본 전략

일부 기법에 대해 간략히 살펴보았으므로, 빈 공간 할당을 위한 기본 전략에 대해 살펴보자. 기본 전략들은 여러분들이 스스로 생각해 낼 수 있을만큼 매우 간단하다. 읽기 전에 한 번 생각해 보라. 모든 대안을 생각해 보았는지 확인하라. 아니면 새로운 정책을 생각했을 수도 있다.

이상적인 할당기는 속도가 빠르고 단편화를 최소로 해야 한다. 불행하게도 할당과 해제 요청 스트림은 무작위, 결국 프로그래머에 의해 결정되기 때문에, 어느 특정 전략도 잘 맞지 않는 입력을 만나면 성능이 매우 좋지 않을 수 있다. 우리는 최선의 정책을 설명하는 것이 아니라 몇 가지 기본 정책에 대해 이야기하고 각각의 장점과 단점을 논의한다.

최적 적합 (Best Fit)

최적 적합 전략은 매우 간단하다. 먼저 빈 공간 리스트를 검색하여 요청한 크기와 같거나 더 큰 빈 메모리 청크를 찾는다. 그 후, 후보자 그룹 중에서 가장 작은 크기의 청크를 반환한다. 이 청크는 최적 청크라고 불린다. 최소 적합이라고도 불릴 수 있다. 빈 공간 리스트를 한 번만 순회하면 반환할 정확한 블럭을 찾을 수 있다.

최적 적합의 배경은 간단하다. 사용자가 요청한 크기에 가까운 블럭을 반환함으로써 최적 적합은 공간의 낭비를 줄이려고 노력한다. 그러나 이에는 비용이 수반된다. 정교하지 않은 구현은 해당 빈 블럭을 찾기 위해 항상 전체를 검색해야 하기 때문에 엄청난 성능 저하를 초래한다.

최악 적합 (Worst Fit)

최악 적합은 최적 적합의 반대 방식이다. 가장 큰 빈 청크를 찾아 요청된 크기 만큼만 반환하고 남는 부분은 빈 공간 리스트에 계속 유지한다. 최악 적합은 최적 적합 방식에서 발생할 수 있는 수많은 작은 청크 대신에 커다란 빈 청크를 남기려고 시도한다. 그러나 다시 한 번 항상 빈 공간 전체를 탐색해야 하기 때문에 이 방법 역시 높은 비용을 지불해야 한다. 설상가상으로 대부분의 연구에서 엄청난 단편화가 발생하면서 오버헤드도 여전히 크다는 것을 보이고 있다.

최초 적합 (First Fit)

최초 적합은 간단하게 요청보다 큰 첫 번째 블럭을 찾아서 요청만큼 반환한다. 먼저와 같이 남은 빈 공간은 후속 요청을 위해 계속 유지된다.

최초 적합은 속도가 빠르다는 것이 장점이다. 원하는 블럭을 찾기 위해 항상 빈 공간 리스트 전체를 탐색할 필요가 없다. 그러나 때때로 리스트의 시작에 크기가 작은 객체가 많이 생길 수 있다. 따라서 할당기가 빈 공간 리스트의 순서를 관리하는 방법이 쟁점이다. 한 가지 방법은 주소-기반 정렬(address-based ordering)을 사용하는 것이다. 리스트를 주소로 정렬하여 병합을 쉽게 하고, 단편화를 감소시킨다.

다음 적합 (Next Fit)

항상 리스트의 처음부터 탐색하는 대신 다음 적합 알고리즘은 마지막으로 찾았던 원소를 가리키는 추가의 포인터를 유지한다. 아이디어는 빈 공간 탐색을 리스트 전체에 더 균등하게 분산시키는 것이다. 리스트의 첫 부분에만 단편이 집중적으로 발생하는 것을 방지한다. 이러한 접근 방식은 전체 탐색을 하지 않기 때문에 최초 적합의 성능과 비슷하다.

예제

위에서 언급한 전략이 동작하는 몇 가지 예를 보도록 하겠다. 크기가 각각 10, 30, 및 20인 세 개의 원소를 가진 빈 공간 리스트를 생각해 보자(여기서는 헤더와 다른 세부 사항은 무시하고 전략이 동작하는 방법에 대해서만 초점을 맞춘다).

크기 15인 요청이 들어왔다고 가정하자. 최적 적합 방법은 전체 리스트를 검색하여 요청을 만족시킬 수 있는 청크 중 가장 작은 20을 선택한다. 할당 후 빈 공간 리스트는 다음과 같다:

이 예에서와 같이, 최적 적합의 경우에는 종종 작은 빈 청크가 남는다. 최악 적합 방식은 유사하지만 대신 가장 큰 청크를 찾는 데 이 예에서는 30이다. 할당 후 빈 공간 리스트는 다음과 같다.

이 예에서 최초 적합 전략은 최악 적합 전략과 같은 결과를 도출한다. 요청을 충족시킬 수 있는 첫 번째 빈 블럭을 찾았다. 차이점은 탐색 비용이다. 최적 적합과 최악 적합은 리스트 전체를 탐색한다. 최초 적합은 단지 적합한 청크를 발견할 때까지만 빈 청크를 검사하기 때문에 탐색 비용이 감소된다.

살펴본 예들은 할당 정책들의 동작을 피상적으로 간단히 보여 준다. 전략에 대한 심도있는 이해를 위해서는 실제 워크로드를 대상으로 그리고 더 복잡한 할당기 동작(예, 병합)에 대한 더 상세한 분석이 필요하다.

17.4 다른 접근법

위에서 설명한 기본적인 접근 방식 외에도 메모리 할당을 향상시키기 위한 기술과 알고리즘이 제안되었다. 그 중 몇 가지를 여기서 소개한다. 단순한 최적 적합 할당에 그치지 않고 그 이상에 대해서 생각해 보도록 하는 것이 목적이다.

개별 리스트

한 동안 유행했던 방법은 별도의 개별 리스트(segregated list)를 사용하는 것이다. 기본적인 아이디어는 간단하다. 특정 응용 프로그램이 한두 가지 자주 요청하는 크기가 있다면, 그 크기의 객체를 관리하기 위한 별도의 리스트를 유지하는 것이다. 다른 모든 요청은 더 일반적인 메모리 할당기에게 전달된다.

이 방법의 장점은 분명하다. 특정 크기의 요청을 위한 메모리 청크를 유지함으로써 단편화 가능성을 상당히 줄일 수 있다. 요청된 크기의 청크만이 존재하기 때문에 복잡한 리스트 검색이 필요하지 않으므로 할당과 해제 요청을 신속히 처리할 수 있다.

다른 좋은 아이디어처럼, 이 방법은 시스템에 새로운 문제를 야기한다. 예를 들어, 지정된 크기의 메모리 풀과 일반적인 풀에 얼마만큼의 메모리를 할당해야 하는가? 특수 목적 할당기인 슬랩 할당기(slab allocator)는 이 문제를 더 나은 방법으로 해결한다. 슬랩 할당기는 뛰어난 엔지니어인 Jeff Bonwick에 의해 Solaris 커널을 위하여 설계되었다 [Bon94].

커널이 부팅될 때 커널 객체를 위한 여러 객체 캐시(object cache)를 할당한다. 커널 객체란 락, 파일 시스템 아이노드 등 자주 요청되는 자료 구조들을 일컫는다. 객체 캐시는 지정된 크기의 객체들로 구성된 빈 공간 리스트이고 메모리 할당 및 해제 요청을 빠르게 서비스 하기 위해 사용된다. 아이노드들로 구성된 객체 캐시가 있고, 락 구조만을 담고 있는 객체 캐시도 있다. 기존에 할당된 캐시 공간이 부족하면 상위 메모리 할당기에게 추가 슬랩을 요청한다. 요청의 전체 크기는 페이지 크기의 정수배이다. 반대로, 슬랩 내 객체들에 대한 참조 횟수가 0이 되면 상위 메모리 할당기는 이 슬랩을 회수할 수 있다. VM 시스템이 더 많은 메모리를 필요할 때 실제 회수가 일어난다.

슬랩 할당 방식은 빈 객체들을 사전에 초기화된 상태로 유지한다는 점에서 개별 리스트 방식보다 우수하다. Bonwick은 자료 구조의 초기화와 반납에는 많은 시간이 소요된다는 것을 발견하였다 [Bon94]. 반납된 객체들을 초기화된 상태로 리스트에 유지하여 슬랩 할당기는 객체당 잦은 초기화와 반납의 작업을 피할 수 있어서 오버헤드를 현저히 감소시킨다.

여담 : 위대한 엔지니어는 정말 위대하다

여기서 얘기한 슬랩 할당기뿐 아니라 ZFS라는 놀라운 파일 시스템의 발명을 주도한 Jef Bonwick 같은 엔지니어는 실리콘 밸리의 심장이다. 거의 모든 위대한 작품이나 기술 뒤에는 재주, 능력과 헌신이 평균 이상인 인간(또는 인간의 소그룹)이 있다. Facebook의 Mark Zuckerberg는 "예외적인 사람들은 보통 사람보다 조금 우수한 것이 아니다. 그들은 100배 우수하다."라고 말한다. 이것이 왜 아직도 오늘날 하나 또는 두 사람이 세상의 모습을 영원히 바꾸는 회사를 시작할 수 있는 이유이다(Google, Apple 또는 Facebook을 생각해 보라). 열심히 노력하면 당신도 그러한 "100×" 사람이 될지도 모른다. 그런 사람이 못 된다면 그런 사람과 함께 일을 하라. 대부분의 사람이 한 달 동안 배우는 것보다 더 많은 것을 하루 동안에 배우게 될 것이다. 그것도 실패하면 슬퍼하라.

버디 할당

빈 공간의 합병은 할당기의 매우 중요한 기능이기 때문에 합병을 간단히 하는 방법들이 설계되었다. 하나의 좋은 예가 이진 버디 할당기(binary buddy allocator)이다 [Kno65]. 빈 메모리는 처음에 개념적으로 크기 $2^N$인 하나의 큰 공간으로 생각된다. 메모리 요청이 발생하면, 요청을 충족시키기에 충분한 공간이 발견될 때까지(그리고 더 분할하면 공간이 너무 작아져서 요청을 만족시킬 수 없을 때까지) 빈 공간을 2개로 계속 분할한다. 이 시점에서 요청된 블럭이 사용자에게 반환된다. 64 KB 빈 공간에서 7 KB 블럭을 할당하는 예가 있다.

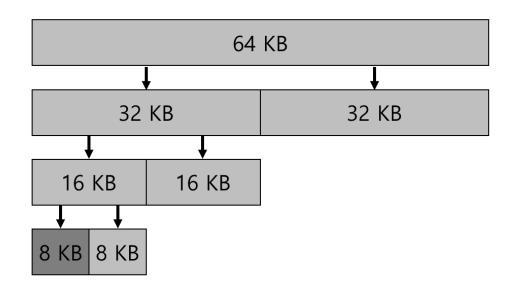
그림 17.8 버디 할당

이 예에서 가장 왼쪽의 8 KB 블럭이 할당되고 (짙은 회색으로 표시) 사용자에게 반환된다. 이 방식은 2의 거듭제곱 크기 만큼의 블럭만 할당할 수 있기 때문에 내부 단편화로 고생할 수 있다는 점에 유의하라.

버디 할당의 아름다움은 블럭이 해제될 때에 있다. 8 KB 블럭을 빈 공간 리스트에 반환하면 할당기는 "버디" 8 KB가 비어 있는지 확인한다. 비어 있다면 두 블럭을 병합하여 16 KB 블럭으로 만든다. 할당기는 다음 16 KB의 버디가 비어 있는지 확인한다. 비어 있다면 이 두 블럭을 다시 합병한다. 이 재귀 합병 과정은 트리를 따라 전체 빈 공간이 복원되거나 버디가 사용 중이라는 것이 밝혀질 때까지 계속 올라간다.

버디 할당이 잘 작동하는 이유는 특정 블럭의 버디를 결정하는 것이 쉽다는 데 있다. 앞에서 빈 공간에 존재하는 블럭의 주소를 한 번 생각해 보자. 각 버디 쌍의 주소는 오직

한 비트만 다르다. 어느 위치의 비트가 다른가는 버디 트리의 수준에 따라 달라진다. 이제 이진 버디 할당 기법의 동작에 대한 기본 사항을 알게 되었다. 더 자세한 사항에 대해서는 Wilson의 요약 문서를 보라 [RWi+95].

기타 아이디어

앞에서 설명한 접근 방식들의 한 가지 문제점은 확장성이다. 빈 공간들의 개수가 늘어남에 따라 리스트 검색이 매우 느려질 수 있다. 좀 더 정교한 할당기는 복잡한 자료 구조를 사용하여 이 비용을 줄인다. 단순함과 성능을 교환한다. 균형 이진 트리(balanced binary tree), 스플레이 트리(splay tree), 또는 부분 정렬 트리(partially ordered tree)가 좋은 예이다 [RWi+95].

현대의 시스템은 멀티프로세서 및 멀티쓰레드로 작동된다. 멀티프로세서를 위해 할당기를 최적화하는 노력들이 많이 있었다. Berger [Ber+00]와 Evans [Eva06]가 좋은 예이다. 자세한 내용에 대해서는 그들을 참조하라.

이들은 오랜 시간 발전한 수천 개의 할당기 아이디어 중 두 개에 해당한다. 관심이 있다면 직접 읽어 보기 바란다. 그럴 수 없다면 실제는 어떤가를 이해하기 위해 glibc의 할당기가 어떻게 작동하는지에 대해서 읽어라 [Spl15].

17.5 요약

이 장에서 가장 기본적인 형태의 메모리 할당기를 논의하였다. 이러한 할당기는 많은 곳에 존재한다. 우리가 작성한 모든 C 프로그램뿐 아니라 운영체제에도 존재한다. 여느 시스템과 마찬가지로, 이러한 시스템을 구축하는 데 많은 선택 사항들이 있다. 할당기에 들어오는 워크로드를 정확히 이해할수록, 그 워크로드에 대해 더 잘 작동하도록 조정할 수 있다. 다양한 워크로드에 대해 빠르고 효율적이고 확장성이 좋은 (scalable) 할당기를 만드는 일은 현대 컴퓨터 시스템의 숙제이다.

참고 문헌

[Ber+00] "Hoard: A Scalable Memory Allocator for Multithreaded Applications" Emery D. Berger, Kathryn S. McKinley, Robert D. Blumofe, and Paul R.Wilson ASPLOS-IX, November 2000

Berger와 동료들의 멀티프로세서 시스템을 위한 훌륭한 할당기. 단지 흥미로운 논문을 넘어서 실제 사용 중인 할당기.

[Bon94] "The Slab Allocator: An Object-Caching Kernel Memory Allocator" Jeff Bonwick

USENIX '94

운영체제 커널을 위한 할당기를 구축하는 방법과 자주 사용되는 특정 객체의 크기에 대해 특화시키는 방법의 훌륭한 예에 관한 멋진 논문.

[Eva06] "A Scalable Concurrent malloc(3) Implementation for FreeBSD"

Jason Evans

April 2006

url: http://people.freebsd.org/%CB%9Cjasone/jemalloc/bsdcan2006/jemalloc.pdf

멀티프로세서에서 사용될 실제 현대의 할당기 구축 방법에 관한 상세한 관찰. "jemalloc" 할당기는 현재 FreeBSD, NetBSD, Mozilla Firefox, 및 Facebook에서 널리 사용 중에 있다.

[Kno65] "A Fast Storage Allocator"

Kenneth C. Knowlton

Communications of the ACM, Volume 8, Number 10, October 1965

버디 할당에 대한 표준 참고 문헌. 이상한 사실: Knuth는 이 아이디어에 대한 공을 Knowlton 이 아니라 노벨상 수상 경제학자인 Harry Markowitz에 돌린다. 또 다른 이상한 사실: Knuth 는 그의 모든 이메일을 비서를 통하여 주고 받는다. 그는 직접 이메일을 보내지 않고 비서에게 보낼 이메일을 말하고 비서가 전송 작업을 수행한다. 마지막 Knuth에 관한 사실: 그는 이 책을 조판하는 데 사용된 도구인 TeX을 만들었다. 그것은 환상적인 소프트웨어 작품이다³.

[RWi+95] "Dynamic Storage Allocation: A Survey and Critical Review"

Paul R.Wilson, Mark S. Johnstone, Michael Neely, and David Boles International Workshop on Memory Management

Kinross, Scotland, September 1995

메모리 할당의 여러 측면에 관한 훌륭하고 지대한 영향을 준 조사. 이 짧은 장 안에 모든 것을 담기에는 너무 자세한 내용.

[Spl15] "Understanding glibc malloc"

Sploitfun

February, 2015

https://sploitfun.wordpress.*com/2015/02/10/understanding-glibc-malloc/*에는 glibc malloc이 어떻게 동작하는지를 놀라울 정도로 자세하고 깊이 있게 연구한 내용을 담고 있는 매우 멋진 문서.

숙제

malloc.py 프로그램은 이 장에서 논의한 간단한 빈 공간 할당기의 동작을 탐색할 수 있게 한다. 그 기본 동작에 대한 자세한 사항은 README를 참조하시오

문제

1. 먼저 무작위 할당과 해제를 생성하기 위하여 -n 10 -H 0 -p BEST -s 0 플래그를 주고 실행시켜라. alloc()과 free()가 무엇을 반환할지 예측할 수 있는가? 각 요청 후의 빈 공간 리스트의 상태를 추측할 수 있는가? 시간이 지남에 따라 빈 공간 리스트에 대해 무엇을 알 수 있는가?
2. 빈 공간 리스트를 탐색하기 위하여 최악 적합 정책을 사용할 때 결과는 어떻게 달라지는가 (-p WORST)? 무엇이 바뀌는가?
3. 최초 적합을 사용한 경우는 어떤가 (-p FIRST)? 최초 적합을 사용하면 속도 향상은 어떻게 되는가?
4. 위 질문에 대해, 몇몇 정책의 경우 리스트의 정렬 순서가 빈 위치를 찾는 데 걸리는 시간에 영향을 준다. 다른 빈 공간 리스트의 순서 (-l ADDRSORT, -l SIZESORT+, -l SIZESORT-)를 사용하여 정책과 리스트 순서가 서로 어떤 영향을 주는지 관찰하라.
5. 빈 공간의 합병은 매우 중요할 수 있다. 무작위 할당의 개수를 늘려라 (-n 1000). 시간이 지날수록 요청의 개수가 많아지면 어떤 현상이 발생하는가? 병합이 있는 채로 그리고 없는 채로 실행하라 (-C 플래그가 없거나 있거나). 출력에 어떤 차이를 볼 수 있는가? 각각의 경우의 시간이 지남에 따라 빈 공간 리스트의 크기는 얼마나 커지는가? 이 경우 리스트의 정렬 순서가 중요한가?
6. 할당 비율 -P를 50 이상으로 변경하면 어떤 일이 일어날까? 100에 가까울수록 할당에는 어떤 일이 발생하는가? 0에 가까워진다면?
7. 심하게 단편화된 빈 공간을 만들어 내려면 어떤 종류의 요구를 생성할 수 있는가? 단편화된 리스트를 생성하기 위하여 -A 플래그를 사용하라. 다른 정책과 옵션이 빈 공간 리스트의 구조에 어떤 영향을 주는지 관찰하라.

Footnotes

1. 거의 80 페이지에 달하기 때문에 관심을 끌 것이다! ↩

2. 이 논의는 헤더가 없다고 가정한다. 비현실적인 가정이지만 당분간 논의를 간단하게 하기 위해 가정한다. ↩

3. 실제로는 LATEX을 사용하였다. LATEX은 Lamport가 TeX에 추가 기능으로 만든 것으로 거의 같다고 할 수 있다. ↩