제20장: 페이징: 더 작은 테이블
페이징의 두 번째 문제점은 페이지 테이블의 크기이다. 페이지 테이블이 크면 많은 메모리 공간을 차지한다. 배열 형태를 가지는 선형 페이지 테이블(linear page table)을 예로 들어 보자. 전술한 바와 같이1 선형 페이지 테이블은 상당히 커질 수가 있다. 페이지 크기가 이고, 페이지 테이블의 각 항목은 4바이트인 32비트 주소 공간()을 가정해 보자. 주소 공간에는 대략 백만 개()의 가상 페이지가 존재할 것이다. 여기에 페이지 테이블 항목의 크기를 곱하면 (4바이트 백만 개), 페이지 테이블의 크기가 된다. 하나의 페이지 테이블 크기가 약 4 MB가 된다. 또 하나 잊으면 안되는 사실이 있다! 일반적으로 각 프로세스는 자기 자신의 페이지 테이블을 갖는다. 백 개의 프로세스가 실행 중이라면 (현대 시스템에서 드물지 않다), 페이지 테이블이 100개 존재하며, 400 MB의 메모리가 필요하다. 이런 엄청난 메모리 부담을 해결할 수 있는 기술을 모색해 보자. 다양한 해법들이 존재한다. 핵심 질문은 아래와 같이 요약될 수 있다.
핵심 질문: 페이지 테이블을 어떻게 더 작게 만들까 단순한 배열 기반의 페이지 테이블은(흔히 선형 페이지 테이블이라고 불림) 크기가 크며 일반적인 시스템에서 메모리를 과도하게 차지한다. 어떻게 페이지 테이블의 크기를 줄일 수 있을까? 주요 개념들로는 무엇이 있는가? 새로운 자료 구조들은 어떤 비효율성을 갖는가?
20.1 간단한 해법: 더 큰 페이지
페이지 테이블의 크기를 간단하게 줄일 수 있는 방법이 한 가지 있다. 페이지 크기를 증가시키면 된다. 32비트 주소 공간에서, 이번에는 16 KB 페이지를 가정해 보자. 이제는 18비트의 VPN과 14비트의 오프셋을 갖게 된다. 각 PTE (4바이트)의 크기가 모두 동일하다면, 페이지 테이블에 개의 항목이 있으며, 페이지 테이블의 총 크기는 1 MB가 된다. 기존 페이지 테이블 대비 크기가 1/4로 감소된다 (당연하다. 테이블의 크기가 1/4로 감소한 것은 페이지 크기가 정확히 4배 증가했기 때문이다).
여담: 멀티 페이지 크기 (Multiple Page Sizes) 많은 컴퓨터 구조들 (예: MIPS, SPARC, x86-64)이 멀티 크기 페이지를 지원한다는 것을 기억하자. 일반적으로, 작은 (4 KB 또는 8 KB) 페이지 크기가 사용된다. 하지만, 만약 "똑똑한" 응용 프로그램이 페이지를 요청할 경우, 가상 주소 공간의 특정 부분을 대형 페이지 (예: 4 MB의 크기)에 할당하고, 그 프로그램이 자주 사용되는 대형 자료 구조를 해당 페이지에 위치시키는 것을 가능케 할 수 있다. 대형 페이지를 사용하므로 TLB에서 하나의 항목만 사용한다. 이러한 대형 페이지는 데이터베이스 관리 시스템과 고성능 프로그램에서 흔히 사용된다. 멀티 페이지 크기를 사용하는 주요 이유는 페이지 테이블의 공간을 절약하려는 것은 아니다. TLB 미스를 줄여 프로그램이 주소 공간을 접근할 수 있도록 하기 위해서이다. 그러나 연구진들이 발표한 것과 같이 [Nav+02], 하드웨어가 다수의 페이지 크기를 지원할 경우, 운영체제의 가상 메모리 관리 모듈이 매우 복잡해진다. 대형 페이지를 간단히 사용하는 방법으로, 추가 인터페이스를 정의하여, 응용 프로그램이 대형 페이지를 직접 요청할 수 있도록 할 수 있다.
페이지 크기의 증가는 부작용을 수반한다. 가장 큰 문제는 페이지 내부의 낭비 공간이 증가하는 것이다. 이를 내부 단편화(internal fragmentation)라 한다 (할당된 페이지 내부에서 낭비가 발생하기 때문이다). 응용 프로그램이 여러 페이지를 할당받았지만, 할당받은 페이지의 일부분만 사용하는 터에, 결국 컴퓨터 시스템의 메모리가 금방 고갈되는 현상이 발생한다. 이런 연유에서, 많은 컴퓨터 시스템들이 비교적 작은 페이지들을 사용한다. 일반적으로 4 KB (x86) 또는 8 KB (SPARCv9)를 사용한다. 페이지 테이블 크기를 감소시키는 우리의 당면 문제는 그리 쉽게 해결되지 않을 것이다.
20.2 하이브리드 접근 방법: 페이징과 세그멘트
인생의 어떤 일을 함에 있어 좋은 방법이 두 가지 있다면, 그 두 방법을 잘 조합하여, 장점만을 취할 수는 없는지도 검토해 보아야 한다. 두 가지 방법을 조합하는 것을 하이브리드(hybrid)라고 부른다. 예를 들면, 초콜릿과 피넛 버터를 섞어만든 Reese 사의 Peanut Butter Cup [M28]이 있는데, 사람들은 왜 피넛 버터와 초콜릿 중 하나만 먹을까?2
Multics의 창시자 Jack Dennis는 Multics 가상 메모리 시스템을 구축하는 데 있어, 비슷한 아이디어가 떠올랐다 [M07]. Dennis는 페이징과 세그멘테이션을 결합하여 페이지 테이블 크기를 줄이는 아이디어를 내었다. 선형 페이지 테이블의 동작을 면밀히 분석해 보면, 페이징과 세그멘테이션을 효과적으로 결합할 수 있다는 사실을 발견할 수 있다. 힙과 스택에서 실제로 전체 공간 중 작은 부분만 사용되는 경우를 생각해 보자.
그림 20.1: 1 KB 페이지들로 이루어진 16 KB 주소 공간
| VPN | PFN | 접근 | 유효 | 보호 |
|---|---|---|---|---|
| 0 | 10 | 1 | 1 | r-x |
| 1 | - | 0 | - | - |
| 2 | - | 0 | - | - |
| 3 | - | 0 | - | - |
| 4 | 23 | 1 | 1 | rw- |
| 5 | - | 0 | - | - |
| ... | ... | ... | ... | ... |
| 14 | 28 | 1 | 1 | rw- |
| 15 | 4 | 1 | 1 | rw- |
그림 20.2: 16 KB 주소 공간을 위한 페이지 테이블
1 KB 크기의 페이지를 갖는 16 KB의 주소 공간을 예로 들겠다 (그림 20.1). 이 주소 공간을 위한 페이지 테이블은 그림 20.2에 나타나 있다.
이 예제에서 한 개의 코드 페이지 (VPN 0)가 물리 페이지 10번, 그리고 한 개의 힙 페이지 (VPN 4)가 23번 물리 페이지에 매핑되어 있다. 가상 주소 공간의 끝부분에 두 개의 스택 페이지 (VPN 14와 15) 가 물리 페이지 28번과 4번에 매핑되어 있다. 그림에서 보는 바와 같이, 페이지 테이블 대부분이 비어있다. 엄청난 낭비가 발생한다. 16 KB 크기의 아주 작은 주소 공간에서 발생한 상황이다. 32비트 주소 공간용 페이지 테이블에서 비슷한 상황이 발생할 것을 상상해 보자. 골치 아픈 일이다.
결합 방식을 생각해 보자. 프로세스의 전체 주소 공간을 위해 하나의 페이지 테이블을 두는 대신, 논리 세그멘트마다 따로 페이지 테이블을 두면 어떨까? 이 예제에서는 세 개의 페이지 테이블이 있을 수 있다. 코드, 힙 그리고 스택 세그멘트에 대해 페이지 테이블을 각각 두는 것이다.
세그멘테이션에서는 세그멘트의 물리 주소 시작 위치를 나타내는 베이스(base) 레지스터, 그리고 크기를 나타내는 바운드(bound) 또는 리미트(limit) 레지스터가 있다. 우리의 결합 방식에서도 MMU에 비슷한 구조를 사용한다. 베이스 레지스터는 세그멘트 시작 주소를 가리키는 것이 아니라 세그멘트의 페이지 테이블의 시작 주소를 갖는다. 바운드 레지스터는 페이지 테이블의 끝을 나타내기 위해서 사용한다.
명확하게 하기 위해 간단한 예를 들어 보자. 4 KB 페이지를 갖는 32비트 가상 주소 공간이 4개의 세그멘트로 나뉘어 있다고 가정하자. 이 예제에서는 세 개의 세그멘트만 사용하도록 하겠다. 하나는 코드를 위해서, 다른 하나는 힙을 위해서 그리고 또 하나는 스택을 위해서 사용한다.
소속 세그멘트를 나타내기 위해 상위 두 비트를 사용한다. 미사용 세그멘트는 00으로, 01은 코드를 그리고 10은 힙, 스택은 11을 나타낸다고 가정하자. 가상 주소는 다음과 같이 표현될 수 있다.
| 31 30 | 29 ... 12 | 11 ... 0 |
|---|---|---|
| Seg | VPN | Offset |
하드웨어에 세 개의 베이스/바운드 레지스터 쌍이 코드와 힙 그리고 스택을 위해서 존재한다고 가정한다. 실행 중인 프로세스에서, 각 세그멘트의 베이스 레지스터는 각 세그멘트 페이지 테이블의 시작 물리 주소를 갖게 된다. 이 시스템에서 모든 프로세스들은 세 개의 페이지 테이블을 갖는다. 문맥 교환 시, 이 레지스터들은 새로 실행되는 프로세스의 페이지 테이블의 위치값으로 변경된다.
TLB 미스가 발생하면 (하드웨어 기반 TLB를 가정한다. 즉, TLB 미스를 하드웨어가 처리한다), 하드웨어는 세그멘트 비트 (SN)을 사용하여 어떤 베이스와 바운드 쌍을 사용할지 결정한다. 하드웨어는 그 레지스터에 들어 있는 물리 주소를 VPN과 다음과 같은 형식으로 조작하여 페이지 테이블 항목 (PTE)의 주소를 얻는다.
SN = (VirtualAddress & SEG_MASK) >> SN_SHIFT
VPN = (VirtualAddress & VPN_MASK) >> VPN_SHIFT
AddressOfPTE = Base[SN] + (VPN * sizeof(PTE))
동작 순서가 눈에 익숙하다. 앞에서 살펴보았던 선형 페이지 테이블의 작동과 거의 동일하다. 유일한 차이가 있다면 하나의 페이지 테이블 베이스 레지스터를 사용하는 대신 세 개 중의 하나의 세그멘트 베이스 레지스터를 사용하는 것이다.
하이브리드 기법에서 핵심은 세그멘트마다 바운드 레지스터가 따로 존재한다는 것이다. 각 바운드 레지스터의 값은 세그멘트의 최대 유효 페이지의 개수를 나타낸다. 예를 들어, 첫 세 개의 페이지들 (0, 1, 그리고 2)을 코드 세그멘트로서 사용 중이라면, 코드 세그멘트 페이지 테이블은 세 개의 항목만 할당을 받을 수 있을 것이고 바운드 레지스터는 3으로 설정된다. 해당 세그멘트의 범위가 넘어가는 곳에 대한 메모리 접근은 예외를 발생시키고, 해당 프로세스는 종료될 것이다. 이와 같은 방식으로, 하이브리드 기법은 선형 페이지 테이블에 비해 메모리 사용을 개선시킬 수 있다. 스택과 힙 사이의 할당되지 않은 페이지들은 페이지 테이블 상에서 (유효하지 않다는 것을 표시하기 위해서) 더 이상 공간을 차지하지 않는다.
하이브리드를 사용하자 두 개의 괜찮은 그리고 상반되는 아이디어가 있다면, 두 방식의 장점을 모두 가져올 수 있도록 두 방식을 혼합하는 하이브리드를 만들 수 있는지 늘 살펴보아야 한다. 하이브리드 옥수수종을 예로 들면 자연적으로 자라나는 종에 비해 좀 더 강인하다고 알려져 있다. 물론, 모든 하이브리드 기법들이 좋은 아이디어는 아니다. 지돈크 (Zeedonk), 또는 존키 (Zonkey)는 얼룩말과 당나귀 사이에서 태어난 동물이다. 그런 생물이 존재하는지 믿지 못하겠다면 찾아보자. 놀랄 것이다.
하지만, 이 기법 역시 문제가 없는 것은 아니다. 첫째, 여전히 세그멘테이션을 사용해야 한다; 이 전에 언급했듯이, 세그멘테이션은 주소 공간의 사용에 있어 특정 패턴을 가정하기 때문에 우리가 원하는 만큼은 유연하지가 못하다. 큰 공간을 커버하지만, 드문드문 사용되는 (sparsely used) 힙의 경우에는 여전히 페이지 테이블의 낭비를 면치 못할 수가 있다. 둘째로, 하이브리드 기법은 외부 단편화를 유발한다. 하이브리드 방식에서는 페이지 테이블 크기에 제한이 없으며 다양한 크기를 갖는다. 물론, 페이지 테이블의 크기는 페이지 테이블 항목 크기의 정수배가 되어야 한다. 때문에, 메모리 상에서 페이지 테이블용 공간을 확보하는 것이 더 복잡하다. 이런 이유로, 페이지 테이블 크기를 감소시키는 더 나은 방법을 찾는 노력들이 지속되었다.
20.3 멀티 레벨 페이지 테이블
세그멘테이션을 사용하지 않고 페이지 테이블 크기를 줄이는 방법에 대해서 생각해 보자. 어떻게 하면 사용하지 않는 주소 공간을 페이지 테이블에서 제거할 수 있을까? 이번에 소개할 기법은 멀티 레벨 페이지 테이블이다. 멀티 레벨 페이지 테이블에서는 선형 페이지 테이블을 트리 구조로 표현한다. 매우 효율적이기 때문에 많은 현대 시스템에서 사용되고 있다 (예: x86 [BO10]). 이 기법을 좀 더 상세히 설명하도록 하겠다.
멀티 레벨 페이지 테이블의 기본 개념은 간단하다. 먼저, 페이지 테이블을 페이지 크기의 단위로 나눈다. 그 다음, 페이지 테이블의 페이지가 유효하지 않은 항목만 있으면, 해당 페이지를 할당하지 않는다. 페이지 디렉터리(page directory)라는 자료 구조를 사용하여 페이지 테이블 각 페이지의 할당 여부와 위치를 파악한다. 페이지 디렉터리는 페이지 테이블을 구성하는 각 페이지의 존재 여부와 위치 정보를 가지고 있다.
그림 20.3의 예제를 보자. 좌측 그림은 전형적인 선형 페이지 테이블이다. 페이지 테이블의 중앙부에 해당하는 주소 공간은 사용되고 있지 않다. 그러나 페이지 테이블에서 항목들이 할당되어 있다 (페이지 테이블의 가운데 두 페이지). 우측은 동일한 주소 공간을 다루는 멀티 레벨 페이지 테이블이다. 페이지 디렉터리에는 두 개의 유효한 페이지가 있다 (첫 번째와 마지막). 유효 페이지 두 개는 메모리에 존재한다. 이 예를 통해 멀티 레벨 페이지 테이블의 동작을 좀 더 쉽게 알 수 있다. 선형 페이지 테이블에서 사용되었던 페이지들이 더 이상 필요없고, 페이지 디렉터리를 이용하여 페이지 테이블의 어떤 페이지들이 할당되었는지를 관리한다.
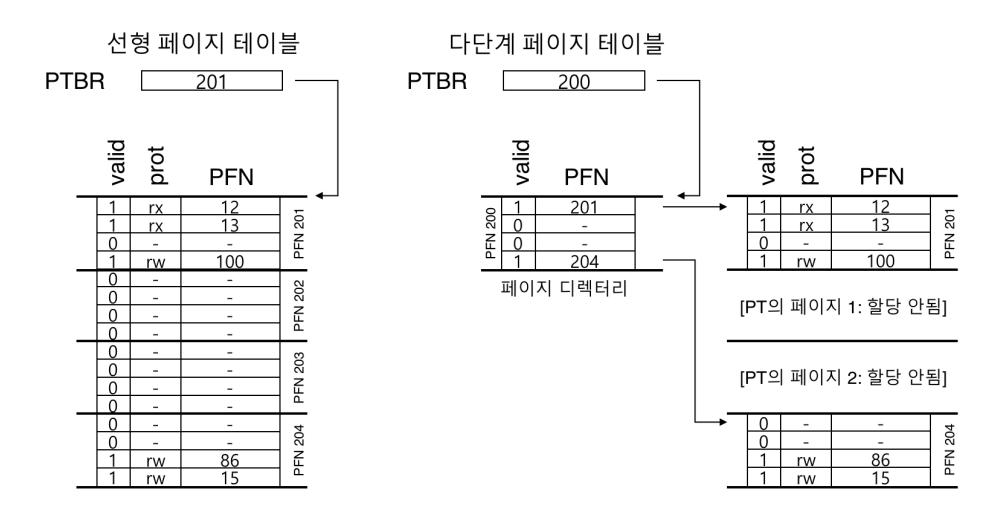그림 20.3: 선형 (좌) 그리고 멀티 레벨 (우) 페이지 테이블
간단한 2단계 테이블에서, 페이지 디렉터리의 각 항목은 페이지 테이블의 한 페이지를 나타낸다. 페이지 디렉터리는 페이지 디렉터리 항목(page directory entries, PDE)들로 구성된다. 각 항목 (PDE)의 구성은 페이지 테이블의 각 항목 (Page Table Entry)과 유사하다. 유효(valid) 비트와 페이지 프레임 번호(page frame number, PFN)를 갖고 있다. 실제 구현에 따라 추가 구성 요소가 존재할 수 있다. 하지만, PTE의 유효 비트와 PDE의 유효 비트는 약간 다르다. PDE 항목이 유효하다는 것은, 그 항목이 가리키고 있는 (PFN을 통해서) 페이지들 중 최소한 하나가 유효하다는 것을 의미한다. 즉, PDE가 가리키고 있는 페이지 내의 최소한 하나의 PTE의 valid bit가 1로 설정되어 있다. 만약 PDE의 항목이 유효하지 않다면 (즉, 0이라면), PDE는 실제 페이지가 할당되어 있지 않은 것이다.
멀티 레벨 페이지 테이블은 이제까지 언급된 다른 기법들에 비해 몇 가지 장점이 있다. 첫째, 멀티 레벨 테이블은 사용된 주소 공간의 크기에 비례하여 페이지 테이블 공간이 할당된다. 그렇기 때문에, 보다 작은 크기의 페이지 테이블로 주소 공간을 표현할 수 있다.
두 번째, 페이지 테이블을 페이지 크기로 분할함으로써 메모리 관리가 매우 용이하다. 페이지 테이블을 할당하거나 확장할 때, 운영체제는 free 페이지 풀에 있는 빈 페이지를 가져다 쓰면 된다. 멀티 레벨 페이징을 단순한 선형 페이지 테이블 방식과 비교해 보자. 선형 페이지 테이블의 각 항목은 해당 가상 페이지의 물리 페이지 주소를 가지고 있다 (즉, 디스크로 스왑되지 않는다). 선형 페이지 테이블은 연속된 물리 메모리 공간을 차지한다. 큰 페이지 테이블 (4 MB라고 하자)의 경우, 해당 크기의 연속된 빈 물리 메모리를 찾는 것이 쉽지 않다. 멀티 레벨 페이징에서는 페이지 디렉터리를 사용하여 각 페이지 테이블 페이지들의 위치를 파악한다. 페이지 테이블의 각 페이지들이 물리 메모리에 산재해 있더라도 페이지 디렉터리를 이용하여 그 위치를 파악할 수 있으므로, 페이지 테이블을 위한 공간 할당이 매우 유연하다.
시간과 공간 간의 절충점에 대해 이해하자 자료 구조 설계 시, 구현에서 시간과 공간의 소요 시간을 적절히 절충 (time-space trade-offs)해야 한다. 일반적으로 자료 구조에 접근 속도를 향상시키려면, 해당 구조를 위해 공간을 더 사용해야 한다. 한 가지 유의해야 할 사항이 있다. 멀티 레벨 테이블에는 추가 비용이 발생한다. TLB 미스 시, 주소 변환을 위해 두 번의 메모리 로드가 발생한다 (페이지 디렉터리와 PTE 접근을 위해 각각 한 번씩). 선형 페이지 테이블에서는 한 번의 접근만으로 주소 정보를 TLB로 탑재한다. 멀티 레벨 테이블은 시간 (페이지 테이블 접근 시간)과 공간 (페이지 테이블 공간)을 상호 절충 (time-space trade-offs)한 예라 할 수 있다. 페이지 테이블 크기를 줄이는 데 성공하였으나, 대신 메모리 접근 시간이 증가했다. TLB 히트 시 (대부분 메모리 접근은 TLB 히트이다) 성능은 동일하지만, TLB 미스 시에는 두 배의 시간이 소요된다.
또 하나의 단점은 복잡도이다. 페이지 테이블 검색이 단순 선형 페이지 테이블의 경우보다 더 복잡해진다. 검색을 하드웨어로 구현하느냐 혹은 운영체제로 구현하느냐 여부와는 무관하다. 대부분의 경우, 성능 개선이나 부하 경감을 위해, 우리는 보다 복잡한 기법을 도입한다. 멀티 레벨 페이지 테이블의 경우에는 메모리 자원의 절약을 위해, 페이지 테이블 검색을 좀 더 복잡하게 만들었다.
멀티 레벨 페이징 예제
멀티 레벨 페이지 테이블의 개념을 이해하기 위해서 예제를 하나 살펴보자. 64바이트 페이지를 갖는 16 KB 크기의 작은 주소 공간을 생각해 보자. 14비트 가상 주소 공간이다. VPN에 8비트, 페이지 오프셋에 6비트가 필요하다. 선형 페이지 테이블은 (256)개 엔트리로 구성된다. 주소 공간에서 작은 부분만 사용된다 하더라도, 선형 페이지 테이블의 크기는 변하지 않는다. 그림 20.4는 이 구조를 갖는 주소 공간의 예시를 나타낸다.
- 이 예제에서는, 가상 페이지 0과 1은 코드, 가상 페이지 4와 5는 힙 그리고 가상 페이지 254와 255는 스택으로 사용된다. 주소 공간의 나머지 페이지들은 미사용 중이다.
- 이 주소 공간을 2단계 페이지 테이블로 구성해 보자. 선형 페이지 테이블을 페이지 단위로 분할한다. 전체 테이블은 (이 예제에서) 총 256개의 항목을 갖고 있다는 것을 상기하자. 각 PTE는 4바이트라 가정한다. 페이지 테이블의 크기는 1 KB (256 4 바이트)이다. 페이지가 64바이트라고 하면 1 KB의 페이지 테이블은 16개의 64바이트 페이지들로 분할된다. 각 페이지에는 16개의 PTE가 있다.
이제 VPN으로부터 페이지 디렉터리 인덱스를 추출하고, 페이지 테이블의 각 페이지 위치를 파악하는 법을 살펴보자. 페이지 디렉터리, 페이지 테이블의 페이지들 모두 항목의 배열이라는 것을 기억해야 한다. VPN을 이용하여 인덱스를 구성하는 법만 찾으면 된다.
먼저 페이지 디렉터리의 인덱스를 만들어보자. 예제의 작은 페이지 테이블은 256개의 항목으로 16개의 페이지로 나뉘어 있다. 페이지 디렉터리는 페이지 테이블의 각 페이지마다 하나씩 있어야하기 때문에 총 16개의 항목이 있어야 한다. 결과적으로 VPN의 4개의 비트를 사용하여 디렉터리를 구성하며, 여기서는 VPN의 상위 4비트를 다음과 같이 사용한다.
| VPN | 내용 |
|---|---|
| 0000 0000 | code |
| 0000 0001 | code |
| 0000 0010 | (free) |
| 0000 0011 | (free) |
| 0000 0100 | heap |
| 0000 0101 | heap |
| 0000 0110 | (free) |
| 0000 0111 | (free) |
| ... | 모두 free |
| 1111 1100 | (free) |
| 1111 1101 | (free) |
| 1111 1110 | stack |
| 1111 1111 | stack |
그림 20.4: 64바이트 페이지들로 이루어진 16 KB 주소 공간
복잡도를 주의하자 시스템 설계자들은 시스템 복잡도의 증가를 주의해야 한다. 좋은 시스템 개발자는 주어진 작업을 처리하기 위한 최소한의 복잡도를 갖는 시스템을 만든다. 예를 들어, 디스크 공간이 풍부하다면 공간 사용을 최소화하기 위한 파일 시스템을 설계해서는 안 된다. 마찬가지로, 프로세서가 빠르다면 어떤 작업을 처리하기 위해 운영체제 내에 이해하기 쉬운 모듈을 작성하는 것이 CPU에 최적화되어 있고 치밀하게 짜여진 코드를 사용하는 것보다 더 좋다. 너무 성급하게 최적화한 코드는 다른 형태에서 불필요한 복잡도를 추가하지 않도록 예의주시하자. 그러한 시스템은 더 이해하기 어려우며 관리와 디버깅을 어렵게 만든다. 앙투안 드 생텍쥐페리 (Antoine de Saint-Exupery)는 이런 유명한 말을 남겼다. "완벽함은 무엇인가 더 추가할 것이 없을 때 얻어지는 것이 아니라 더 이상 뺄 것이 없을 때 마침내 얻어진다." 그가 기록하지 않은 부분은 "완벽함에 대해서 이야기 하는 것이 실제로 달성하는 것보다 더 쉽다."는 것이다.
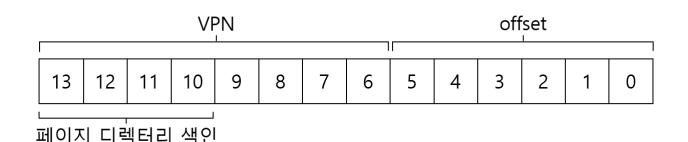
VPN에서 페이지-디렉터리 인덱스(page-directory index, 짧게 PDIndex라고 하자)를 추출하고 나면 PDEAddr = PageDirBase + (PDIndex * sizeof(PDE)) 라는 간단한 식을 사용하여 페이지-디렉터리 항목 (page-directory entry, PDE)의 주소를 찾을 수 있다. 이렇게 페이지 디렉터리가 구성이 되며, 이것을 활용하여 계속해서 주소 변환 과정을 분석하도록 한다.
페이지-디렉터리의 해당 항목이 무효 (invalid)라고 표시되어 있으면, 이 주소 접근은 유효하지 않다. 예외가 발생한다. 해당 PDE가 유효하다면 추가 작업을 해야 한다. 구체적으로 살펴보자. 이 페이지 디렉터리 항목이 가리키고 있는 페이지 테이블의 페이지에서 원하는 페이지 테이블 항목 (page table entry, PTE)을 읽어 들이는 것이 목표다. 이 PTE를 찾기 위해서 VPN의 나머지 비트들을 사용한다.
이 페이지-테이블 인덱스(page-table index, 짧게 PTIndex라고 하자)는 페이지 테이블 자체 인덱스로 사용된다. PTE의 주소를 다음과 같이 계산한다.
PTEAddr = (PDE.PFN << SHIFT) + (PTIndex * sizeof(PTE))
PTE의 주소를 생성하기 위해서는 페이지-디렉터리 항목에서 얻은 페이지-프레임 번호 (page-frame number, PFN)를 먼저 좌측 쉬프트 연산하고 그 값을 페이지 테이블 인덱스에 합산한다.
이 모든 것이 제대로 작동하는지를 보기 위해, 멀티 레벨 페이지 테이블에 실제 값들을 넣은 후에 하나의 가상 주소를 변환해 보자. 이 예제를 위해 페이지 디렉터리에서부터 시작해 보자 (그림 20.5의 좌측).
이 그림에서 각 페이지 디렉터리 항목 (PDE)은 주소 공간의 페이지 테이블의 페이지에 대해 무엇인가를 기술하고 있다. 이 예제에서는 주소 공간에 두 개의 유효한 영역이 있으며 (처음과 끝에), 그리고 그 사이는 무효한 매핑들이 존재한다.
물리 페이지 100에 (페이지 테이블의 0번째 페이지의 물리 프레임 번호), 페이지 테이블의 첫 16개 항목이 존재한다. 이 항목들은 가상 주소 공간의 첫 16개 페이지에 대한 물리 주소를 가진다. 그림 20.5의 가운데 열이 해당 페이지의 내용이다.
페이지 테이블의 첫 번째 페이지에는 첫 16개의 VPN과 물리 페이지 주소가 있다. 이 예제에서는 VPN 0과 1이 유효하고 (코드 세그멘트), 4와 5도 유효하다 (힙). 그러므로 테이블에는 각 페이지들의 매핑 정보가 있다. 그 외의 나머지 엔트리들은 무효로 표기되어 있다.
PFN 101에 다른 유효 페이지들에 대한 정보가 들어있다. 이 페이지에는 가상 주소 공간의 마지막 16개의 VPN에 대한 매핑이 담겨 있다. 그림 20.5의 우측에 상세 내용이 있다.
이 예제에서는, VPN 254와 255가 유효 페이지이다. 이들은 스택에 해당한다. 이 예제를 통해서 멀티 레벨 인덱스 구조가 공간을 얼마큼 절약할 수 있는지를 확인할 수 있다. 선형 페이지 테이블의 열여섯 개의 페이지들을 모두 할당하는 대신 단지 세 개만 할당하였다. 페이지 디렉터리를 위해서 한 페이지, 그리고 유효한 매핑 정보를 갖고 있는 페이지 테이블 내의 두 부분을 위해 두 페이지를 할당하였다. 더 큰 (32비트 또는 64비트) 주소 공간에서는 더 많은 공간이 절약된다.
| 페이지 디렉터리 | | | PT의 페이지 (@PFN:100) | | | PT의 페이지 (@PFN:101) | | | :-------------: | :-------: | :-: | :--------------------: | :------: | :------: | :--------------------: | :------: | -------- | | PFN | 유효? | | PFN | 유효 | prot | PFN | 유효 | prot | | 100 | 1 | | 10 | 1 | r-x | | 0 | | | | 0 | | 23 | 1 | r-x | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | 80 | 1 | rw- | | 0 | | | | 0 | | 59 | 1 | rw- | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | | 0 | | | | 0 | | | 0 | | 55 | 1 | rw | | 101 | 1 | | | 0 | | 45 | 1 | rw- |
그림 20.5: 페이지 디렉터리와 페이지 테이블의 일부
마지막으로 최종 주소 변환을 해 보자. VPN 254의 0번째 바이트를 가리키는 주소는 다음과 같다. 0x3F80 또는 이진수로 11 1111 1000 0000 이다.
페이지 디렉터리 내에서 각 항목을 가르키기 위해 VPN의 상위 4비트를 사용하였다. 1111은 페이지 디렉터리의 마지막 엔트리다 (0부터 시작했다면 15번째가 된다). 페이지 디렉터리의 15번째 엔트리에는 물리 프레임 주소 101이 저장되어 있다. VPN의 다음의 4비트를 (1110)을 인덱스로 사용하여, 페이지 테이블의 해당 페이지에서 원하는 PTE를 찾는다. 1110는 101번 페이지의 16개 항목 중에 마지막에서 두 번째 항목이다. 여기에 55가 저장되어 있다. 종합하면 가상 주소 페이지 254 (1111 1110)는 물리 페이지 55에 존재한다. 오프셋 000000과 PFN 55(또는 헥사로 0x37)를 결합하여 다음과 같이 물리 주소를 구할 수 있으며, 해당 메모리를 접근하는 데 사용된다.
PhysAddr = (PTE.PFN << SHIFT) + offset = 00 1101 1100 0000 = 0x0DC0
이제 페이지 디렉터리를 사용하여 페이지 테이블의 페이지를 가리키는 2단계 페이지 테이블에 대한 개념이 어느 정도 이해되었을 것이다. 곧 구체화하겠다. 2단계 페이지 테이블이 충분하지 않을 때가 있다!
20.4 2단계 이상 사용하기
지금까지는 멀티 레벨 페이지 테이블은 페이지 디렉터리와 페이지 테이블의 2개 단계를 가정하였다. 경우에 따라서 트리의 단계를 더 증가시키는 것도 가능하다 (그리고 사실, 그래야 할 필요가 있다).
간단한 예제를 통해 2단계 이상의 멀티 레벨 테이블에 대해 알아보자. 이 예제에서는 512바이트 페이지와 30비트 가상 주소 공간을 가정한다. 가상 주소는 21비트의 가상 페이지 번호와 9비트의 오프셋을 갖게 된다.
멀티 레벨 페이지 테이블의 목적은 페이지 테이블의 모든 분할된 부분들이 단일 페이지 크기에 맞도록 하는 것이다. 만약 페이지 디렉터리가 너무 커지면, 어떻게 될까?
멀티 레벨 테이블에서 몇 단계를 둘지 정하기 위해서는 먼저 한 페이지에 몇 개의 페이지 테이블 항목을 저장할 수 있을지를 계산해야 한다. 페이지 크기가 512바이트이고 PTE의 크기가 4바이트라고 가정하면 한 페이지에 128개의 PTE를 넣을 수 있다. 페이지 테이블의 페이지를 인덱스로 쓰려면, VPN의 하위 7비트 ()가 필요하다.
페이지 디렉터리를 위해서 몇 개의 비트가 남았는지를 이 그림에서 알 수 있다. 14개의 비트가 남는다. 2단계 페이지를 사용한다면, 페이지 디렉터리에 개의 항목이 있게 된다. 페이지 디렉터리를 위해서 128 페이지 분량의 연속된 메모리가 필요하다. 페이지 테이블을 페이지 단위로 나누어 배치할 수 있도록 하는 멀티 레벨 페이지 테이블의 근본 취지가 훼손된 셈이다.
이 문제를 해결하기 위해서, 페이지 디렉터리 자체를 멀티 페이지들로 나누어 트리의 단계를 늘리도록 한다. 그리고 페이지 디렉터리의 페이지들을 가리킬 수 있도록 그 위에 새로운 페이지 디렉터리를 추가한다. 결과적으로 다음과 같이 가상 주소를 분할할 수 있다.
이제 가상 주소의 최상위 비트들을 (그림에서 PD Index 0) 사용하여 상위 단계의 페이지 디렉터리에서 엔트리를 찾는다. 이 인덱스를 사용하여 상위 단계 페이지 디렉터리에서 페이지 디렉터리 항목을 가져온다. 만약 유효하다면, 상위 단계 페이지 디렉터리에서 얻은 물리 주소와 두 번째 단계의 페이지 디렉터리 인덱스 (PD Index 1)를 결합하여 페이지 테이블 인덱스가 존재한 물리 페이지를 구한다. 해당 페이지가 유효할 경우, 최종적으로, PTE 주소는 2번째 단계의 페이지 디렉터리 항목에서 얻은 페이지 테이블의 물리 주소와 페이지 테이블 인덱스를 결합하여 구한다. 실제 주소를 구하는 데 드는 작업이 상당하다. 멀티 레벨 페이지 테이블 사용 시 수반되는 작업이기도 하다.
변환 과정: TLB를 기억하자
2단계 페이지 테이블 사용 시, 전체 주소 변환 과정을 알고리즘 형태로 요약 정리해 보자 (그림 20.6). 이 그림은 모든 메모리 참조에 대해 하드웨어가 어떤 식으로 동작하는지를 나타낸다(하드웨어 기반 TLB를 가정).
그림에서 볼 수 있듯이, 복잡한 멀티 레벨 페이지 테이블 접근을 거치기 전에, 우선 TLB를 검사한다. 히트가 되면 페이지 테이블을 참조 없이 물리 주소를 직접 구성한다. TLB 미스 시에만, 멀티 레벨 페이지 테이블의 모든 단계를 거쳐 물리 주소를 구하게 된다. 이 알고리즘을 통해 TLB 미스 발생 시, 전통적인 2단계 페이지 테이블의 주소 계산 비용을 볼 수 있다. 주소 변환을 위해 두 번의 추가 메모리 접근이 발생한다.
VPN = (VirtualAddress & VPN_MASK) >> SHIFT
(Success, TlbEntry) = TLB_Lookup(VPN)
if (Success == True) // TLB 히트
if (CanAccess(TlbEntry.ProtectBits) == True)
Offset = VirtualAddress & OFFSET_MASK
PhysAddr = (TlbEntry.PFN << SHIFT) | Offset
Register = AccessMemory(PhysAddr)
else
RaiseException(PROTECTION_FAULT)
else // TLB 미스
// 먼저. 페이지 디렉터리 항목을 얻어야 함
PDIndex = (VPN & PD_MASK) >> PD_SHIFT
PDEAddr = PDBR + (PDIndex * sizeof(PDE))
PDE = AccessMemory(PDEAddr)
if (PDE.Valid == False)
RaiseException(SEGMENTATION_FAULT)
else
// PDE 가 유효함: 이제 페이지 테이블에서 PTE를 가져오자
PTIndex = (VPN & PT_MASK) >> PT_SHIFT
PTEAddr = (PDE.PFN << SHIFT) + (PTIndex * sizeof(PTE))
PTE = AccessMemory(PTEAddr)
if (PTE.Valid == False)
RaiseException(SEGMENTATION_FAULT)
else if (CanAccess(PTE.ProtectBits) == False)
RaiseException(PROTECTION_FAULT)
else
TLB_Insert(VPN, PTE.PFN, PTE.ProtectBits)
RetryInstruction()
그림 20.6: 멀티 레벨 페이지 테이블의 제어 흐름
20.5 역 페이지 테이블
좀 더 획기적인 공간 절약 방법으로 역 페이지 테이블(inverted page table)이 있다. 이 방법에서는 여러 개의 페이지 테이블(시스템의 프로세스당 하나씩) 대신 시스템에 단 하나의 페이지 테이블만 둔다. 페이지 테이블은 물리 페이지를 가상 주소 상의 페이지로 변환한다. 역 페이지 테이블의 각 항목은 해당 물리 페이지를 사용 중인 프로세스 번호, 해당 가상 페이지 번호를 갖고 있다.
페이지 테이블의 목적은 가상 주소를 물리 주소로 변환하는 것이다. 역 페이지 테이블에서는 주소 변환을 위해 전체 테이블을 검색해서 원하는 가상 주소 페이지를 갖는 항목을 찾아야 한다. 순차 탐색은 느리다. 탐색 속도 향상을 위해 주로 해시 테이블을 사용한다. PowerPC는 이 구조를 사용하는 예이다 [JM98].
좀 더 일반적인 시각에서 보자면, 역 페이지 테이블 역시 하나의 자료 구조일 뿐이다. 자료 구조로 다양한 시도를 할 수 있다. 예를 들면 작게도 만들고 크게도 만들 수 있으며 느리게도 빠르게도 만들 수가 있다. 멀티 레벨과 반전된 페이지 테이블들은 할 수 있는 다양한 방법 중 두 가지 예일 뿐이다.
20.6 페이지 테이블을 디스크로 스와핑하기
마지막으로 중요한 가정을 해제하겠다. 이제까지는 페이지 테이블이 커널이 소유하고 있는 물리 메모리 영역에 존재한다고 가정하였다. 페이지 테이블 크기 축소를 위해 많은 시도를 하더라도, 여전히 모든 페이지 테이블을 메모리에 상주시키기에는 양이 너무 클 수도 있다. 그렇기 때문에 어떤 시스템들은 페이지 테이블들을 커널 가상 메모리에 존재시키고, 시스템의 메모리가 부족할 경우, 페이지 테이블들을 디스크로 스왑(swap) 하기도 한다. 이 부분에 대해서는 페이지들을 메모리에 탑재하고 제거하는 방법을 이해한 후에, 다시 (구체적으로 VAX/VMS에 대한 사례 연구를 다루는 장에서) 상세히 다루도록 한다.
20.7 요약
페이지 테이블이 실제로 어떻게 구성되었는지를 보았다. 단순한 선형 배열을 사용하는 구조뿐만 아니라 좀 더 복잡한 자료 구조의 형태도 살펴보았다. 테이블을 위한 자료 구조에는 시간과 공간이라는 모순적 선택 사항이 존재한다. 공간을 많이 소모하는 테이블 구조를 사용할수록 TLB 미스의 처리 속도가 빨라지고, 공간을 작게 차지하는 테이블 구조를 사용하면 상황은 반대가 된다. 주어진 제약 조건들을 적절히 고려하여 적합한 자료 구조를 결정해야 한다.
주기억 장치 용량이 작았던 과거 시스템 (많은 과거의 시스템들과 같은)의 경우, 소형 자료 구조의 사용이 현명한 선택이었다. 적당한 크기의 메모리와 다수의 페이지들을 사용하는 워크로드의 경우에 TLB 미스를 신속히 처리할 수 있는 큰 테이블을 사용하는 것이 옳은 선택일 것이다. 소프트웨어로 관리되는 TLB의 경우에는, 전체 자료 구조를 운영체제 개발자가 임의로 그리고 혁신적으로 개발, 그리고 개선할 수 있다. 어떤 새로운 자료 구조가 있을까? 그 새로운 구조는 어떤 문제를 해결하는가? 잠들기 전에 이러한 질문들을 해 보라. 그리고 운영체제 개발자만 꿀 수 있는 큰 꿈을 꾸자.
참고 문헌
[BO10] "Computer Systems: A Programmer's Perspective" Randal E. Bryant and David R. O'Hallaron Addison-Wesley, 2010 아직 멀티 레벨 페이지 테이블에 대한 좋은 일차 참고 문헌을 찾아야 한다. 하지만 Bryant와 O'Hallaron이 쓴 이 엄청난 교재는 멀티 레벨 페이지 테이블을 사용했던 초기의 시스템 중의 하나였던 x86의 세부적인 내용을 다루고 있다. 그리고 갖고 있을만한 좋은 책 중에 하나이기도 하다.
[JM98] "Virtual Memory: Issues of Implementation" Bruce Jacob and Trevor Mudge IEEE Computer, June 1998 여러 다른 시스템들과 각각의 시스템의 메모리 가상화 기법에 대한 포괄적인 조사로서 x86과 PowerPC, MIPS 그리고 다른 컴퓨터 구조에 대한 설명이 상세히 나와 있다.
[LL82] "Virtual Memory Management in the VAX/VMS Operating System" Hank Levy and P. Lipman IEEE Computer, Vol. 15, No. 3, March 1982 운영체제의 고전인 VMS의 실제 가상 메모리 관리자에 대한 아주 훌륭한 논문이다. 너무나 훌륭하기 때문에 앞으로의 몇 장은 이 논문을 기반으로 우리가 여태까지 배운 가상 메모리에 대해서 다시 살펴보도록 하겠다.
[M28] "Reese's Peanut Butter Cups" Mars Candy Corporation. 이 훌륭한 당과류는 1928년에 해리 버넷 리스 (Harry Burnett Reese)에 의해서 만들어진 것으로 보인다. 농업에 종사했던 그는 Milton S. Hershey의 선적 감독 중의 하나였다. 위키페디아에서 적힌 것으로는 그렇다. 그게 사실이라면, Hershey와 Reese는 여느 두 명의 초콜릿 부호들이 그런 것처럼 서로 쳐다도 보기 힘들었을 것이다.
[M07] "Multics: History" url: http://www.multicians.org/history.html 운영체제 역사상 가장 영향력 있었던 시스템 중의 하나인 Multics 시스템에 대한 방대한 양의 역사를 소개하는 놀라운 웹사이트이다. 내용 중 한 구절을 인용한다. "MIT의 Jack Dennis는 Multics가 처음 개발될 때 영향력 있는 구조적 개념들을 제안하는 공헌을 하였다. 그의 공헌 중에는 페이징과 세그멘테이션을 결합하는 개념도 포함된다." (섹션 1.2.1 중에서)
[Nav+02] "Practical, Transparent Operating System Support for Superpages" Juan Navarro, Sitaram Iyer, Peter Druschel, and Alan Cox OSDI '02, Boston, Massachusetts, October 2002 현대의 운영체제에 큰 페이지나 슈퍼페이지들을 포함하기 위해 필요한 모든 상세 정보들을 나타낸 좋은 논문이다. 그렇지만 생각하는 만큼 그렇게 쉬운 것은 아니다.
숙제
멀티 레벨 페이지 테이블이 어떻게 동작하는지를 이해하고 있는지를 확인하기 위한 재미있는 작은 숙제이다. 앞 문장에서 "재미"있다는 표현이 적합한지에 대해서는 논란이 있는 것은 사실이다. 놀랍지 않겠지만, 프로그램의 이름은 paging-multilevel-translate.py이다. README의 상세한 설명을 참고하자.
문제
- TLB 미스에 대해서 하드웨어가 검색을 한다는 가정 하에서 선형 페이지 테이블을 사용하면 페이지 테이블의 위치를 찾기 위해 하나의 레지스터가 필요하다. 2단계 페이지 테이블을 사용하는 경우에는 몇 개의 레지스터가 필요한가? 3단계 페이지 테이블을 사용하는 경우는 몇 개가 필요한가?
- 시뮬레이터를 이용하여 변환을 수행하여 보자. 이때 랜덤 시드는 0과 1 그리고 2를 사용하여 보자.
-c플래그를 사용하여 답이 맞는지 확인해 보자. 각 검색을 수행하기 위해서 몇 번의 메모리 참조가 필요한가? - 캐시 메모리가 어떻게 동작하는지 이해했다고 했을 때, 캐시를 사용하면 페이지 테이블에 대한 메모리 참조는 어떻게 동작할까? 캐시 히트가 많이 생겨날까 (그래서 빠르게 접근될 것인가)? 또는 많은 미스를 만들어 낼까 (그러므로 느리게 접근될 것인가)?